Question

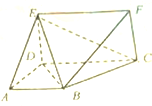如图所示，直角梯形ABCD和矩形CDEF所在的平面互相垂直，AD⊥DC，AB∥DC，AB=AD=DE=1，CD=2．
（1）证明：BD⊥平面BCF；
（2）设二面角A-BE-C的平面角为θ，求cosθ的值．

Answer 1

考点：二面角的平面角及求法,直线与平面垂直的判定

专题：空间角

分析：（1）如图所示，取CD的中点M，连接BM．可得四边形ABMD是平行四边形．可证∠DBC=90°．利用平面ABCD⊥平面
CDEF，可得ED⊥平面ABCD，FC⊥平面ABCD．利用三垂线定理可证BD⊥平面BCF．
（2）通过建立空间直角坐标系，利用平面法向量的夹角即可得出二面角的大小．

解答： （1）证明：如图所示，取CD的中点M，连接BM．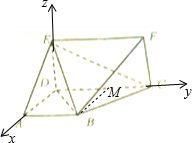
∵DM∥AB，DM=

1

2

CD=AB，
∴四边形ABMD是平行四边形．
∴MB=AD=

1

2

CD．
∴∠DBC=90°．即DB⊥BC．
∵ED⊥DC，平面ABCD⊥平面CDEF，
∴ED⊥平面ABCD．
∵FC∥ED．
∴FC⊥平面ABCD．
∴DB⊥BF．
∵BF∩BC=B．
∴BD⊥平面BCF．
（2）解：如图所示，建立空间直角坐标系．则A（1，0，0），B（1，1，0），C（0，2，0），E（0，0，1）．
∴

AB

=（0，1，0），

BE

=（-1，-1，1），

BC

=（-1，1，0）．
设平面ABE，平面BEC的法向量分别为

n

，

m

．
设

n

=（x，y，z），则

n • AB =y=0 n • BE =-x-y+z=0

，取x=1，解得y=0，z=1．∴

n

=（1，0，1）．
同理可得：

m

=（1，1，2）．
∴cos＜

m

，

n

＞=

m • n

| m || n |

=

3

6 × 2

=

3

2

．
由图可知：二面角A-BE-C的平面角θ为钝角，
∴cosθ=-

3

2

．

点评：本题考查了三垂线定理、线面与面面垂直的判定定理、平行四边形的判定与性质定理、线面角与二面角、勾股定理、直角三角形的边角关系、利用平面法向量的夹角求二面角，考查了空间想象能力，考查了推理能力与计算能力，属于难题．