Question

已知

x2

2

+y²=1的左右焦点分别为F₁、F₂，直线l过点F₁与椭圆交于A、B两点，求△ABF₂面积的最大值．

Answer 1

考点：椭圆的简单性质

专题：圆锥曲线中的最值与范围问题

分析：设直线l的倾斜角为θ，当θ≠

π

2

时，求出△ABF₂的面积，当θ=

π

2

时，求出△ABF₂的面积，比较得出△ABF₂面积的最大值．

解答： 解：如图所示，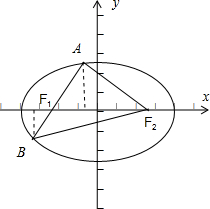
设直线l的倾斜角为θ，当θ≠

π

2

时，不妨设θ∈（0，

π

2

）；
∴l的方程是y=tanθ（x+1），
∴

y=tanθ(x+1) x2 2 +y2=1

；
∵tanθ≠0，消去x，得

1+2tan2θ

tan2θ

y²-

2

tanθ

y-1=0，
∴y₁+y₂=

2

tanθ

×

tan2θ

1+2tan2θ

=

2tanθ

1+2tan2θ

，
y₁y₂=-

tan2θ

1+2tan2θ

；
∴|y₁-y₂|=

(y1+y2)2-4y1y2

=

4tan2θ (1+2tan2θ)2 + 4tan2θ 1+2tan2θ

=

2 2 tanθ• 1 cosθ

1+2tan2θ

=

2 2 sinθ

sin2θ+1

=

2 2

sinθ+ 1 sinθ

；
∵θ∈（0，

π

2

），
∴sinθ+

1

sinθ

＞2，
∴|y₁-y₂|＜

2

，
∴S△ABF2＜

1

2

×2c|y₁-y₂|=

1

2

×2×

2

=

2

；
当θ=

π

2

时，|AB|=2•

b2

a

=2×

1

2

=

2

，
∴S△ABF2=

1

2

•|AB|•2c=

1

2

×

2

×2=

2

；
综上，△ABF₂面积的最大值为

2

．

点评：本题考查了椭圆的定义，计算三角形面积的应用问题，基本不等式的运用问题等综上，是中档题．