题目内容
16.6本不同的书分成3组,一组4本,其余组各1本,共有不同的分法( )| A. | 5种 | B. | 10种 | C. | 15种 | D. | 20种 |
分析 6本不同的书分三份,2份1本,1份4本,其中有均匀分组问题.
解答 解:六本不同的书分成3组,一组4本,其余1本,有$\frac{{C}_{6}^{4}{C}_{2}^{1}{C}_{1}^{1}}{{A}_{2}^{2}}$=15种分堆方法.
故选C.
点评 本题考查排列、组合及简单计数问题,考查计算能力,理解能力,属于基础题.

练习册系列答案
相关题目
6.变量x,y之间的一组相关数据如表所示:
若x,y之间的线性回归方程为$\widehaty$=$\widehatb$x+12.28,则$\widehatb$的值为( )
| x | 4 | 5 | 6 | 7 |
| y | 8.2 | 7.8 | 6.6 | 5.4 |
| A. | -0.92 | B. | -0.94 | C. | -0.96 | D. | -0.98 |
4.用一个平面去截一个四棱锥,截面形状不可能的是( )
| A. | 四边形 | B. | 三角形 | C. | 五边形 | D. | 六边形 |
8.在等差数列{an}中,a1=10,公差为d,前 n项和为Sn,当且仅当n=5 时Sn取得最大值,则d 的取值范围为( )
| A. | $(-\frac{5}{2},-2)$ | B. | $(-∞,-\frac{5}{2}]$ | C. | (-∞,-2] | D. | $[-\frac{5}{2},-2]$ |
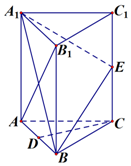 如图,在正三棱柱ABC-A1B1C1中,每条棱长均相等,D为棱AB的中点,E为侧棱CC1的中点.
如图,在正三棱柱ABC-A1B1C1中,每条棱长均相等,D为棱AB的中点,E为侧棱CC1的中点.