题目内容
6.已知函数f(x)=|2x+1|+|2x-3|.(1)求不等式f(x)≤6的解集;
(2)若对任意$x∈[-\frac{1}{2},1]$,不等式f(x)≥|2x+a|-4恒成立,求实数a的取值范围.
分析 (1)通过对x取值的分类讨论,去掉绝对值符号,即可求得不等式f(x)≤6的解集;
(2)利用等价转化思想,可得|2x+a|≤8,从而求出实数a的取值范围.
解答 解:(1)1°当$x≤-\frac{1}{2}$时,-2x-1-2x+3≤6⇒x≥-2;
2°当$-\frac{1}{2}<x<\frac{3}{2}$时,2x+1-2x+3≤6恒成立;
3°当$x≥\frac{3}{2}$时,4x-2≤6⇒x≤2
综上,解集为[-2,2];
(2)f(x)≥|2x+a|-4?|2x+a|≤8
即-8≤2x+a≤8$⇒\left\{\begin{array}{l}a-1≥-8\\ a+2≤8\end{array}\right.$⇒-7≤a≤6.
点评 本题考查绝对值不等式的解法,着重考查等价转化思想、分类讨论思想与综合运算能力,属于中档题.

练习册系列答案
相关题目
16.6本不同的书分成3组,一组4本,其余组各1本,共有不同的分法( )
| A. | 5种 | B. | 10种 | C. | 15种 | D. | 20种 |
14.已知实数x、y满足$\left\{\begin{array}{l}x-y+2≥0\\ x+y≥0\\ 4x-y-1≤0\end{array}\right.$,则z=2x+y的最大值为( )
| A. | -1 | B. | $\frac{6}{5}$ | C. | 5 | D. | 6 |
11.已知m>1,x,y满足约束条件$\left\{\begin{array}{l}x-y+4≥0\\ mx-y+5-m≤0\\ 0≤x≤1\end{array}$,若目标函数z=ax+by(a>0,b>0)的最大值为3,则$\frac{1}{a}$+$\frac{2}{b}$( )
| A. | 有最小值 $\frac{{11+2\sqrt{10}}}{3}$ | B. | 有最大值$\frac{{11+2\sqrt{10}}}{3}$ | ||
| C. | 有最小值$\frac{{11-2\sqrt{10}}}{3}$ | D. | 有最大值$\frac{{11-2\sqrt{10}}}{3}$ |
15.已知a=${∫}_{0}^{1}$xdx,b=${∫}_{0}^{1}$x2dx,c=${∫}_{0}^{1}$$\sqrt{x}$dx,则a,b,c的大小关系是( )
| A. | a<b<c | B. | a<c<b | C. | b<a<c | D. | c<a<b |
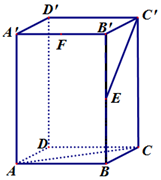 如图长方体ABCD-A'B'C'D'中,AB=BC=1,AA'=2,E、F分别是BB′、A'B'的中点.
如图长方体ABCD-A'B'C'D'中,AB=BC=1,AA'=2,E、F分别是BB′、A'B'的中点.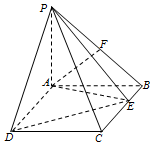 如图,PA⊥平面ABCD,四边形ABCD为矩形,PA=AB=2,AD=4,点F是PB的中点,点E在边BC上移动.
如图,PA⊥平面ABCD,四边形ABCD为矩形,PA=AB=2,AD=4,点F是PB的中点,点E在边BC上移动.