题目内容
4．用一个平面去截一个四棱锥，截面形状不可能的是（ ）| A． | 四边形 | B． | 三角形 | C． | 五边形 | D． | 六边形 |
分析 四棱锥只有五个面，用一个平面去截一个四棱锥，截面形状不可能的是六边形．
解答 解：∵四棱锥只有五个面，
∴用一个平面去截一个四棱锥，截面形状不可能的是六边形，
故选D．
点评 本题考查棱锥的结构特征，考查学生空间想象能力，比较基础．
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
12．
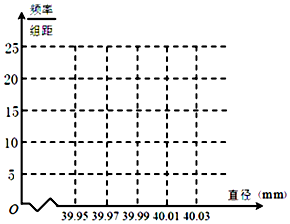某制造厂商10月份生产了一批乒乓球，从中随机抽取n个进行检查，测得每个球的直径（单位：mm），将数据进行分组，得到如下频率分布表：
（1）求a，b，n及p1，p2的值，并画出频率分布直方图（结果保留两位小数）；
（2）已知标准乒乓球的直径为40.00mm，且称直径在[39.99，40.01]内的乒乓球为五星乒乓球，若这批乒乓球共有10000个，试估计其中五星乒乓球的数目．
某制造厂商10月份生产了一批乒乓球，从中随机抽取n个进行检查，测得每个球的直径（单位：mm），将数据进行分组，得到如下频率分布表：| 分组 | 频数 | 频率 |
| [39.95，39.97） | 6 | P1 |
| [39.97，39.99） | 12 | 0.20 |
| [39.99，40.01） | a | 0.50 |
| [40.01，40.03） | b | P2 |
| 合计 | n | 1.00 |
（2）已知标准乒乓球的直径为40.00mm，且称直径在[39.99，40.01]内的乒乓球为五星乒乓球，若这批乒乓球共有10000个，试估计其中五星乒乓球的数目．
某学校1800名学生在一次百米测试中，成绩全部介于13秒与18秒之间，抽取其中50个样本，将测试结果按如下方式分成五组：第一组[13，14]，第二组[14，15），第五组[17，18]，如图是按上述分组方法得到的频率分布直方图．
16．6本不同的书分成3组，一组4本，其余组各1本，共有不同的分法（ ）
| A． | 5种 | B． | 10种 | C． | 15种 | D． | 20种 |
为了了解高中生的身体健康情况，体育局随机抽取了某校20名学生的体育测试成绩，得到如图所示的茎叶图：
14．已知实数x、y满足$\left\{\begin{array}{l}x-y+2≥0\\ x+y≥0\\ 4x-y-1≤0\end{array}\right.$，则z=2x+y的最大值为（ ）
| A． | -1 | B． | $\frac{6}{5}$ | C． | 5 | D． | 6 |