题目内容
7.若将函数f(x)=sin2x+cos2x的图象向左平移φ个单位,所得图象关于y轴对称,则φ的最小正值是$\frac{π}{8}$.分析 将函数f(x)化简后,根据平移变换的规律,得图象关于y轴对称,利用诱导公式可得答案.
解答 解:函数f(x)=sin2x+cos2x=$\sqrt{2}$sin(2x+$\frac{π}{4}$),向左平移φ个单位,可得$\sqrt{2}$sin(2x+2φ+$\frac{π}{4}$),
要使所得图象关于y轴对称,
∴2φ+$\frac{π}{4}$=$\frac{π}{2}+kπ$,即φ=$\frac{π}{8}+\frac{1}{2}kπ$,(k∈Z)
当k=0时,可得φ的最小正值为$\frac{π}{8}$.
故答案为:$\frac{π}{8}$.
点评 函数y=Asin(ωx+φ)的图象变换规律,诱导公式的运用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知a,b∈R+,且$a+b+\frac{1}{a}+\frac{1}{b}=5$,则a+b的取值范围是( )
| A. | [1,4] | B. | [2,+∞) | C. | (2,4) | D. | (4,+∞) |
12.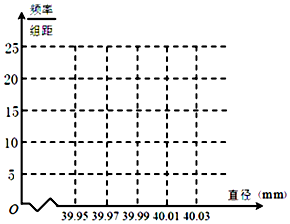 某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:
某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:
(1)求a,b,n及p1,p2的值,并画出频率分布直方图(结果保留两位小数);
(2)已知标准乒乓球的直径为40.00mm,且称直径在[39.99,40.01]内的乒乓球为五星乒乓球,若这批乒乓球共有10000个,试估计其中五星乒乓球的数目.
 某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:
某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:| 分组 | 频数 | 频率 |
| [39.95,39.97) | 6 | P1 |
| [39.97,39.99) | 12 | 0.20 |
| [39.99,40.01) | a | 0.50 |
| [40.01,40.03) | b | P2 |
| 合计 | n | 1.00 |
(2)已知标准乒乓球的直径为40.00mm,且称直径在[39.99,40.01]内的乒乓球为五星乒乓球,若这批乒乓球共有10000个,试估计其中五星乒乓球的数目.
16.6本不同的书分成3组,一组4本,其余组各1本,共有不同的分法( )
| A. | 5种 | B. | 10种 | C. | 15种 | D. | 20种 |
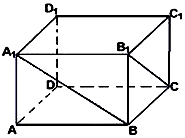 在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,
在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3, 某学校1800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14],第二组[14,15),第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
某学校1800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14],第二组[14,15),第五组[17,18],如图是按上述分组方法得到的频率分布直方图.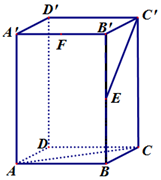 如图长方体ABCD-A'B'C'D'中,AB=BC=1,AA'=2,E、F分别是BB′、A'B'的中点.
如图长方体ABCD-A'B'C'D'中,AB=BC=1,AA'=2,E、F分别是BB′、A'B'的中点.