题目内容
1.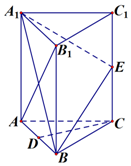 如图,在正三棱柱ABC-A1B1C1中,每条棱长均相等,D为棱AB的中点,E为侧棱CC1的中点.
如图,在正三棱柱ABC-A1B1C1中,每条棱长均相等,D为棱AB的中点,E为侧棱CC1的中点.(1)求证:OD∥平面A1BE
(2)求证:AB1⊥平面A1BE.
分析 (1)设AB1和A1B的交点为O,连接EO,连接OD,易得四边形ECDO为平行四边形,即EO∥CD.得到OD∥平面A1BE.
(2)证明EO⊥AB1. AB1⊥A1B.即可得到AB1⊥平面A1BE
解答  解:(1)设AB1和A1B的交点为O,连接EO,连接OD,因为O为AB1的中点,D为AB的中点,所以OD∥BB1,且$OD=\frac{1}{2}B{B_1}$又E是CC1中点,则EC∥BB1
解:(1)设AB1和A1B的交点为O,连接EO,连接OD,因为O为AB1的中点,D为AB的中点,所以OD∥BB1,且$OD=\frac{1}{2}B{B_1}$又E是CC1中点,则EC∥BB1
且$EC=\frac{1}{2}B{B_1}$,所以EC∥OD且EC=OD.所以四边形ECDO为平行四边形,
所以EO∥CD. …(4分)
又CD?平面A1BE,EO?平面A1BE,则CD∥平面A1BE…(7分)
(2)因为正三棱柱,所以BB1⊥平面ABC.因为CD?平面ABC,
所以BB1⊥CD.由已知得AB=BC=AC,所以CD⊥AB.
所以CD⊥平面A1ABB1由(1)可知EO∥CD,所以EO⊥平面A1ABB1所以EO⊥AB1. …(11分)
因为正三棱柱各棱长相等,所以侧面是正方形,所以AB1⊥A1B.
又EO∩A1B=O,EO?平面A1EB,A1B?平面A1EB.所以AB1⊥平面A1BE. …(14分)
点评 本题考查了空间线面平行、线面垂直的判定,转化思想是解题的关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.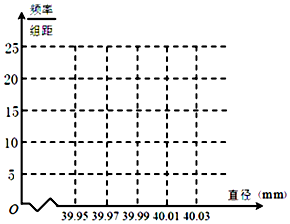 某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:
某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:
(1)求a,b,n及p1,p2的值,并画出频率分布直方图(结果保留两位小数);
(2)已知标准乒乓球的直径为40.00mm,且称直径在[39.99,40.01]内的乒乓球为五星乒乓球,若这批乒乓球共有10000个,试估计其中五星乒乓球的数目.
 某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:
某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:| 分组 | 频数 | 频率 |
| [39.95,39.97) | 6 | P1 |
| [39.97,39.99) | 12 | 0.20 |
| [39.99,40.01) | a | 0.50 |
| [40.01,40.03) | b | P2 |
| 合计 | n | 1.00 |
(2)已知标准乒乓球的直径为40.00mm,且称直径在[39.99,40.01]内的乒乓球为五星乒乓球,若这批乒乓球共有10000个,试估计其中五星乒乓球的数目.
16.6本不同的书分成3组,一组4本,其余组各1本,共有不同的分法( )
| A. | 5种 | B. | 10种 | C. | 15种 | D. | 20种 |
10.如图中的几何体是由下面哪个三角形绕直线旋转所得到的( )
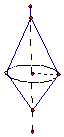

| A. | 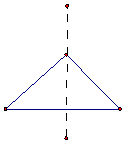 | B. | 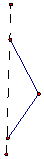 | C. | 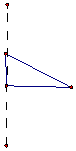 | D. | 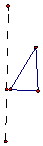 |
11.已知m>1,x,y满足约束条件$\left\{\begin{array}{l}x-y+4≥0\\ mx-y+5-m≤0\\ 0≤x≤1\end{array}$,若目标函数z=ax+by(a>0,b>0)的最大值为3,则$\frac{1}{a}$+$\frac{2}{b}$( )
| A. | 有最小值 $\frac{{11+2\sqrt{10}}}{3}$ | B. | 有最大值$\frac{{11+2\sqrt{10}}}{3}$ | ||
| C. | 有最小值$\frac{{11-2\sqrt{10}}}{3}$ | D. | 有最大值$\frac{{11-2\sqrt{10}}}{3}$ |
 为了了解高中生的身体健康情况,体育局随机抽取了某校20名学生的体育测试成绩,得到如图所示的茎叶图:
为了了解高中生的身体健康情况,体育局随机抽取了某校20名学生的体育测试成绩,得到如图所示的茎叶图: