题目内容
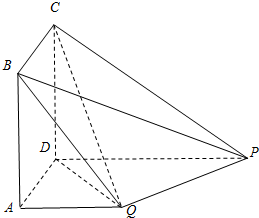 如图,四边形ABCD为矩形,PD⊥平面ABCD,PD∥QA,QA=AD=
如图,四边形ABCD为矩形,PD⊥平面ABCD,PD∥QA,QA=AD=| 1 |
| 2 |
(Ⅰ)证明:平面PQC⊥平面DCQ;
(Ⅱ)若CP与面DQC所成的角的正切值为
| ||
| 5 |
考点:二面角的平面角及求法,平面与平面垂直的判定
专题:空间角
分析:(I)如图所示,取线段PD的中点E,连接QE.可得四边形AQED是平行四边形,∠PQD=90°.可得PD⊥平面ABCD,于是可得CD⊥平面ADPQ.再利用三垂线定理及面面垂直的判定定理即可证明.
(II)由(I)可知:PQ⊥平面CDQ.可得∠PCQ为CP与面DQC所成的角.利用CP与面DQC所成的角的正切值为
,可得CD.可证QA⊥平面ABCD.可得∠QBA为二面角Q-BC-D的平面角.利用直角三角形的边角关系即可得出.
(II)由(I)可知:PQ⊥平面CDQ.可得∠PCQ为CP与面DQC所成的角.利用CP与面DQC所成的角的正切值为
| ||
| 5 |
解答:
(I)证明:如图所示,
取线段PD的中点E,连接QE.
∵DE∥AQ,DE=AQ=
PD,
∴四边形AQED是平行四边形,
∴QE=AD=
PD.
∴∠PQD=90°.
∴PQ⊥QD.
∵PD⊥平面ABCD,
∴PD⊥CD.
又∵CD⊥DA,DA∩DP=D.
∴CD⊥平面ADPQ.
∴PQ⊥QC.
由QD∩QC=Q,
∴PQ⊥平面CDQ.
∴平面PQC⊥平面DCQ.
(II)解:由(I)可知:PQ⊥平面CDQ.
∴∠PCQ为CP与面DQC所成的角.
∵CP与面DQC所成的角的正切值为
,
∴
=
,
由(I)可得PQ=
=DQ,
∴CQ=
.
∴CD=
=
.
∵QA∥PD,
∴QA⊥平面ABCD.
∴∠QBA为二面角Q-BC-D的平面角.
∴tan∠QBA=
=
=
.
∴∠QBA=30°.
∴二面角Q-BC-D为30°.

取线段PD的中点E,连接QE.
∵DE∥AQ,DE=AQ=
| 1 |
| 2 |
∴四边形AQED是平行四边形,
∴QE=AD=
| 1 |
| 2 |
∴∠PQD=90°.
∴PQ⊥QD.
∵PD⊥平面ABCD,
∴PD⊥CD.
又∵CD⊥DA,DA∩DP=D.
∴CD⊥平面ADPQ.
∴PQ⊥QC.
由QD∩QC=Q,
∴PQ⊥平面CDQ.
∴平面PQC⊥平面DCQ.
(II)解:由(I)可知:PQ⊥平面CDQ.
∴∠PCQ为CP与面DQC所成的角.
∵CP与面DQC所成的角的正切值为
| ||
| 5 |
∴
| PQ |
| CQ |
| ||
| 5 |
由(I)可得PQ=
| 2 |
∴CQ=
| 5 |
∴CD=
| CQ2-DQ2 |
| 3 |
∵QA∥PD,
∴QA⊥平面ABCD.
∴∠QBA为二面角Q-BC-D的平面角.
∴tan∠QBA=
| QA |
| AB |
| 1 | ||
|
| ||
| 3 |
∴∠QBA=30°.
∴二面角Q-BC-D为30°.
点评:本题考查了三垂线定理、线面与面面垂直的判定定理、平行四边形的判定与性质定理、线面角与二面角、勾股定理、直角三角形的边角关系,考查了空间想象能力,考查了推理能力与计算能力,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
命题“对任意的x∈R,都有2x2-x+1≥0”的否定是( )
| A、对任意的x∈R,都有2x2-x+1<0 |
| B、存在x0∈R,使得2x02-x0+1<0 |
| C、不存在x0∈R,使得2x02-x0+1<0 |
| D、存在x0∈R,使得2x02-x0+1≥0 |
数列-1,
,-
,
,…的一个通项公式是( )
| 4 |
| 3 |
| 9 |
| 5 |
| 16 |
| 7 |
A、an=(-1)n•
| ||
B、an=(-1)n•
| ||
C、an=(-1)n•
| ||
D、an=(-1)n•
|