题目内容
已知抛物线x2=2y存在两个不同的点M、N关于直线y=kx+3对称,求k的取值范围.
考点:直线与圆锥曲线的关系
专题:直线与圆
分析:设M(x1,
)、N(x2,
)关于已知直线对称,则
=-
=k•
+3=2.由于线段MN的中点必在抛物线内,由此能求出k的取值范围.
| x12 |
| 2 |
| x22 |
| 2 |
| x1+x2 |
| 2 |
| 1 |
| k |
| x12+x22 |
| 4 |
| x1+x2 |
| 2 |
解答:
解:设M(x1,
)、N(x2,
)关于已知直线对称,
=-
,即
=-
又线段MN的中点在直线y=kx+3上,
∴
=k•
+3=2.
由于线段MN的中点必在抛物线内,
有
≥
(
)2=
,即16≥
,
解得k≥
或k≤-
.
| x12 |
| 2 |
| x22 |
| 2 |
| ||||
| x2-x1 |
| 1 |
| k |
| x1+x2 |
| 2 |
| 1 |
| k |
又线段MN的中点在直线y=kx+3上,
∴
| x12+x22 |
| 4 |
| x1+x2 |
| 2 |
由于线段MN的中点必在抛物线内,
有
| x12+x22 |
| 4 |
| 1 |
| 2 |
| x1+x2 |
| 2 |
| (x1+x2)2 |
| 8 |
| 4 |
| k2 |
解得k≥
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查实数的取值范围的求法,是中档题,解题时要认真审题,注意点差法的合理运用.

练习册系列答案
相关题目
设函数f(x)=
则f(
)+f(
)+f(
)+…+f(
)的值为( )
|
| 1 |
| 101 |
| 2 |
| 101 |
| 3 |
| 101 |
| 201 |
| 101 |
| A、199 | B、200 |
| C、201 | D、202 |
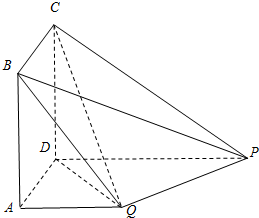 如图,四边形ABCD为矩形,PD⊥平面ABCD,PD∥QA,QA=AD=
如图,四边形ABCD为矩形,PD⊥平面ABCD,PD∥QA,QA=AD=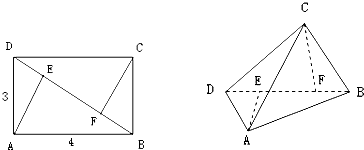 如图,已知矩形ABCD中,AB=2,AD=1,AE⊥BD,CF⊥BD,沿对角线BD把△BCD折起,使二面角C-BD-A的大小为60°,则线段AC的长为
如图,已知矩形ABCD中,AB=2,AD=1,AE⊥BD,CF⊥BD,沿对角线BD把△BCD折起,使二面角C-BD-A的大小为60°,则线段AC的长为