题目内容
已知函数f(x)=2lnx-a(x-
)(a≠0)有两个不同的极值点x1,x2(x1<x2).
(Ⅰ)求a的取值范围;
(Ⅱ)设
<x1<1,求f(x)极小值的取值范围.
| 1 |
| x |
(Ⅰ)求a的取值范围;
(Ⅱ)设
| 1 |
| e |
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)利用导数研究函数的极值,求导,f′(x)=
-a-
=
.令g(x)=-ax2+2x-a,由于函数f(x)=2lnx-a(x-
)有两个极值点?g(x)=0在区间(0,+∞)上有两个实数根.对a分类讨论,解得即可.
(Ⅱ)由(Ⅰ)得0<x1<
<x2,又
<x1<1,对a进行分类讨论,即可求得f(x1)的取值范围.
| 2 |
| x |
| a |
| x2 |
| -ax2+2x-a |
| x2 |
| 1 |
| x |
(Ⅱ)由(Ⅰ)得0<x1<
| 1 |
| a |
| 1 |
| e |
解答:
解:(Ⅰ)f(x)=2lnx-a(x-
)(x>0),f′(x)=
-a-
=
.
令g(x)=-ax2+2x-a,
∵函数f(x)=2lnx-a(x-
)有两个极值点,则g(x)=0在区间(0,+∞)上有两个实数根.
g′(x)=-2ax+2=-2a(x-
),
∴当a<0时,g′(x)>0,则函数g(x)在区间(0,+∞)单调递增,因此g(x)=0在区间(0,+∞)上不可能有两个实数根,应舍去.
当a>0时,令g′(x)=0,解得x=
.
令g′(x)>0,解得0<x<
,此时函数g(x)单调递增;
令g′(x)<0,解得x>
,此时函数g(x)单调递减.
∴当x=
时,函数g(x)取得极大值.
当x趋近于0与x趋近于+∞时,g(x)→-∞,
要使g(x)=0在区间(0,+∞)上有两个实数根,则g(
)=
-a>0,解得0<a<1.
∴实数a的取值范围是(0,1).
(Ⅱ)由(Ⅰ)得0<x1<
<x2,又
<x1<1,
∴当0<a<1时,
<x1<1,∴-1<lnx1<0,
-e<x1-
<0,0<-a(x1-
)<a(e-
)
∴-2<f(x1)=2lnx1-a(x1-
)<a(e-
),即-2<f(x1)<a(e-
).
当1≤a<e时,
<x1<
,∴,∴-1<lnx1<-lna,
-e<x1-
<
-a,a2-1<-a(x1-
)<a(e-
),
∴
-e+a2-1<f(x1)=2lnx1-a(x1-
)<a(e-
)+
-a,即
<f(x1)<a(e-1)+
.
当a≥e时,由0<x1<
<x2,又
<x1<1,可知x1不存在,故f(x1)不存在.
综上所述:当0<a<1时,-2<f(x1)<a(e-
).
1≤a<e时,
<f(x1)<a(e-1)+
.
a≥e时,f(x1)不存在.
| 1 |
| x |
| 2 |
| x |
| a |
| x2 |
| -ax2+2x-a |
| x2 |
令g(x)=-ax2+2x-a,
∵函数f(x)=2lnx-a(x-
| 1 |
| x |
g′(x)=-2ax+2=-2a(x-
| 1 |
| a |
∴当a<0时,g′(x)>0,则函数g(x)在区间(0,+∞)单调递增,因此g(x)=0在区间(0,+∞)上不可能有两个实数根,应舍去.
当a>0时,令g′(x)=0,解得x=
| 1 |
| a |
令g′(x)>0,解得0<x<
| 1 |
| a |
令g′(x)<0,解得x>
| 1 |
| a |
∴当x=
| 1 |
| a |
当x趋近于0与x趋近于+∞时,g(x)→-∞,
要使g(x)=0在区间(0,+∞)上有两个实数根,则g(
| 1 |
| a |
| 1 |
| a |
∴实数a的取值范围是(0,1).
(Ⅱ)由(Ⅰ)得0<x1<
| 1 |
| a |
| 1 |
| e |
∴当0<a<1时,
| 1 |
| e |
| 1 |
| e |
| 1 |
| x1 |
| 1 |
| x1 |
| 1 |
| e |
∴-2<f(x1)=2lnx1-a(x1-
| 1 |
| x1 |
| 1 |
| e |
| 1 |
| e |
当1≤a<e时,
| 1 |
| e |
| 1 |
| a |
| 1 |
| e |
| 1 |
| x1 |
| 1 |
| a |
| 1 |
| x1 |
| 1 |
| e |
∴
| 1 |
| e |
| 1 |
| x1 |
| 1 |
| e |
| 1 |
| a |
| 1-e2+(a2-1)e |
| e |
| e-a2 |
| ae |
当a≥e时,由0<x1<
| 1 |
| a |
| 1 |
| e |
综上所述:当0<a<1时,-2<f(x1)<a(e-
| 1 |
| e |
1≤a<e时,
| 1-e2+(a2-1)e |
| e |
| e-a2 |
| ae |
a≥e时,f(x1)不存在.
点评:本题考查了利用导数研究函数的单调性极值,考查了等价转化方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
已知M>0,N>0,log4M=log6N=log9(M+N),则
的值为( )
| N |
| M |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设函数f(x)=
则f(
)+f(
)+f(
)+…+f(
)的值为( )
|
| 1 |
| 101 |
| 2 |
| 101 |
| 3 |
| 101 |
| 201 |
| 101 |
| A、199 | B、200 |
| C、201 | D、202 |
下面命题中为假命题的是( )
| A、?x∈R,3x>0 |
| B、?α,β∈R,使sin(α+β)=sinα+sinβ |
| C、“x>2”是“x2-3x+2>0”的充分不必要条件 |
| D、命题“?x∈R,x2+1>3x”的否定是“?x∈R,x2+1<3x” |
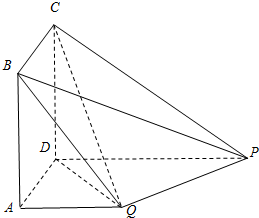 如图,四边形ABCD为矩形,PD⊥平面ABCD,PD∥QA,QA=AD=
如图,四边形ABCD为矩形,PD⊥平面ABCD,PD∥QA,QA=AD=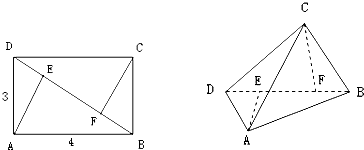 如图,已知矩形ABCD中,AB=2,AD=1,AE⊥BD,CF⊥BD,沿对角线BD把△BCD折起,使二面角C-BD-A的大小为60°,则线段AC的长为
如图,已知矩形ABCD中,AB=2,AD=1,AE⊥BD,CF⊥BD,沿对角线BD把△BCD折起,使二面角C-BD-A的大小为60°,则线段AC的长为