题目内容
数列-1,
,-
,
,…的一个通项公式是( )
| 4 |
| 3 |
| 9 |
| 5 |
| 16 |
| 7 |
A、an=(-1)n•
| ||
B、an=(-1)n•
| ||
C、an=(-1)n•
| ||
D、an=(-1)n•
|
考点:数列的概念及简单表示法
专题:等差数列与等比数列
分析:利用由数列-1,
,-
,
,….可知:奇数项的符号为“-”,偶数项的符号为“+”,其分母为奇数2n-1,分子为n2.即可得出.
| 4 |
| 3 |
| 9 |
| 5 |
| 16 |
| 7 |
解答:
解:由数列-1,
,-
,
,…
可知:奇数项的符号为“-”,偶数项的符号为“+”,
其分母为奇数2n-1,分子为n2.
∴此数列的一个通项公式an=(-1)n•
.
故选:A.
| 4 |
| 3 |
| 9 |
| 5 |
| 16 |
| 7 |
可知:奇数项的符号为“-”,偶数项的符号为“+”,
其分母为奇数2n-1,分子为n2.
∴此数列的一个通项公式an=(-1)n•
| n2 |
| 2n-1 |
故选:A.
点评:本题考查了通过观察分析猜想归纳即可得出数列的通项公式,属于基础题.

练习册系列答案
相关题目
若{a2,0,-1}={a,b,0},则a2014+b2014的值为( )
| A、0 | B、1 | C、-1 | D、2 |
下面命题中为假命题的是( )
| A、?x∈R,3x>0 |
| B、?α,β∈R,使sin(α+β)=sinα+sinβ |
| C、“x>2”是“x2-3x+2>0”的充分不必要条件 |
| D、命题“?x∈R,x2+1>3x”的否定是“?x∈R,x2+1<3x” |
已知函数f(x)=
,则f(f(π))=( )
|
| A、1 | B、0 | C、0或1 | D、不确定 |
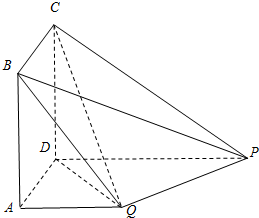 如图,四边形ABCD为矩形,PD⊥平面ABCD,PD∥QA,QA=AD=
如图,四边形ABCD为矩形,PD⊥平面ABCD,PD∥QA,QA=AD= 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<