题目内容
在△ABC中,角A、B、C成等差数列,a、b、c分别为角A、B、C的对边,sinAsinC=cos2B,S△ABC=4
,求a,b,c的值.
| 3 |
考点:余弦定理,正弦定理
专题:解三角形
分析:根据A、B、C成等差数列,求出B的值,由
=
=
①,ac=16②,求出b的值,根据a2+c2=64解出a,c的值即可.
| ac |
| b2 |
| cos2B |
| sin2B |
| 1 |
| 3 |
解答:
解:∵A、B、C成等差数列,
∴2B=A+C,由A+B+C=180°,解得:B=60°,
∵
=
=
,
∴sinA=
sinB,sinC=
sinB,
又sinAsinC=cos2B,
∴
sinB•
sinB=cos2B,
∴
=
=
①,
而S△ABC=4
=
acsinB,
∴ac=16②,
由①②得:b=4
,
由b2=a2+c2-2accosB,得:a2+c2=64③,
由②③得:
或
,
∴a=2
-2
,b=4
,c=2
+2
,
或a=2
+2
,b=4
,c=2
-2
.
∴2B=A+C,由A+B+C=180°,解得:B=60°,
∵
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
∴sinA=
| a |
| b |
| c |
| b |
又sinAsinC=cos2B,
∴
| a |
| b |
| c |
| b |
∴
| ac |
| b2 |
| cos2B |
| sin2B |
| 1 |
| 3 |
而S△ABC=4
| 3 |
| 1 |
| 2 |
∴ac=16②,
由①②得:b=4
| 3 |
由b2=a2+c2-2accosB,得:a2+c2=64③,
由②③得:
|
|
∴a=2
| 6 |
| 2 |
| 3 |
| 6 |
| 2 |
或a=2
| 6 |
| 2 |
| 3 |
| 6 |
| 2 |
点评:本题考查了解三角形问题,考查了正弦定理,余弦定理,三角形的面积公式,是一道中档题.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
已知函数f(x)=
的定义域为[2,3],则实数m的值为( )
| -x2+mx-6 |
| A、5 | B、-5 | C、10 | D、-10 |
设函数f(x)=
则f(
)+f(
)+f(
)+…+f(
)的值为( )
|
| 1 |
| 101 |
| 2 |
| 101 |
| 3 |
| 101 |
| 201 |
| 101 |
| A、199 | B、200 |
| C、201 | D、202 |
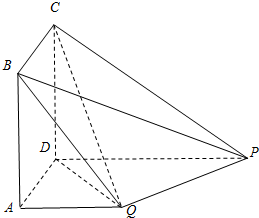 如图,四边形ABCD为矩形,PD⊥平面ABCD,PD∥QA,QA=AD=
如图,四边形ABCD为矩形,PD⊥平面ABCD,PD∥QA,QA=AD=