题目内容

已知a＞0，函数y=x+
a2
x
在x∈（1，+∞）上为增函数，求a的取值范围．
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：先求出函数的导数，得到不等式，解出即可．
解答： 解：∵y′=1-
a2
x2
＞0在（1，+∞）恒成立，
∴x2＞a2，∴a＜x，而x＞1，∴a≤1，
故a的取值范围是（0，1]．
点评：本题考查了函数的单调性问题，考查了不等式的解法，是一道基础题．
练习册系列答案
相关题目
已知函数f（x）=
lnx-x
x
．
（Ⅰ）求点（1，f（1））处的切线方程；
（Ⅱ）求函数f（x）的单调区间；
（Ⅲ）设m＞0，求f（x）在[m，2m]上的最大值．
已知函数f（x）=x2+abx+a+2b．且a、b均为非负数，若f（0）=4，则f（1）的最大值为
 
．
已知函数f（x）=
a
a2-1
•（ax-a-x）（a＞0且a≠1），讨论f（x）的单调性．
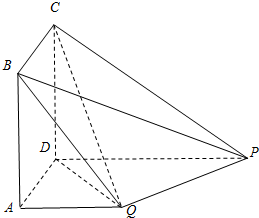如图，四边形ABCD为矩形，PD⊥平面ABCD，PD∥QA，QA=AD=
1
2
PD=1．
（Ⅰ）证明：平面PQC⊥平面DCQ；
（Ⅱ）若CP与面DQC所成的角的正切值为
10
5
，求二面角Q-BC-D的大小．
已知函数f（x）=
ax+b
1+x2
是定义在（-1，1）上的奇函数，且f（
1
3
）=
3
5
．
（1）确定函数f（x）的解析式；
（2）用定义证明f（x）在（-1，1）上是增函数；
（3）解不等式f（t-1）+f（2t）＜0．
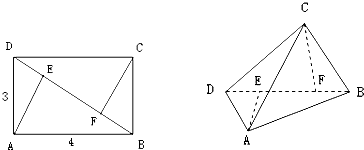如图，已知矩形ABCD中，AB=2，AD=1，AE⊥BD，CF⊥BD，沿对角线BD把△BCD折起，使二面角C-BD-A的大小为60°，则线段AC的长为
 
．
如图，半径为30cm的圆形（O为圆心）铁皮上截取一块矩形材料OABC，其中点B在圆弧上，点A，C在两半径上，现将此矩形材料卷成一个以AB为母线的圆柱形罐子的侧面（不计剪裁和拼接损耗），设OB与矩形材料的边OA的夹角为θ，圆柱的体积为Vcm3．
（Ⅰ）求V关于θ的函数关系式，并写出定义域；
（Ⅱ）求圆柱形罐子体积V的最大值．
若{a2，0，-1}={a，b，0}，则a2014+b2014的值为（　　）
A、0B、1C、-1D、2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网