Question

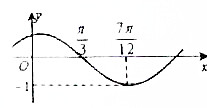已知函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|＜

π

2

）的图象如图所示．
（1）求A、ω及φ的值；
（2）若α∈（-

π

2

，0），且f（

α

2

+

π

12

）=

5

13

，求tanα的值．

Answer 1

考点：正弦函数的图象

专题：三角函数的图像与性质

分析：（1）由图象的顶点坐标求出A，由周期求出ω，通过图象经过（

π

3

，0），求出φ．
（2）由（1）得f（x）=sin（2x+

π

3

），代入值得到cosα=

5

13

，根据α∈（-

π

2

，0），得到sinα=-

12

13

，继而求出tanα的值．

解答： 解：（1）由函数的图象可得A=1，T=4×（

7π

12

-

π

3

）=π，T=

2π

ω

，
解得ω=2．
图象经过（

π

3

，0），0=sin（2×

π

3

+φ），|φ|＜

π

2

），
φ=

π

3

，
（2）由（1）得f（x）=sin（2x+

π

3

），
∴f（

α

2

+

π

12

）=sin（α+

π

6

+

π

3

）=cosα=

5

13

，
∵α∈（-

π

2

，0），
∴sinα=-

12

13

，
∴tanα=

sinα

cosα

=-

12

5

点评：本题主要考查由函数y=Asin（ωx+φ）的部分图象求函数的解析式，注意函数的周期的求法，考查计算能力．