题目内容
已知点P是直线3x+4y+5=0上的动点,点Q为圆(x-2)2+(y-2)2=4上的动点,则|PQ|的最小值为( )
A、
| ||
| B、2 | ||
C、
| ||
D、
|
考点:直线与圆的位置关系
专题:直线与圆
分析:根据直线和圆的位置关系,求出圆心到直线的距离,即可得到结论.
解答:
解:由圆的标准方程(x-2)2+(y-2)2=4得圆心坐标为C(2,2),半径R=2,
圆心到直线的距离d=
=
,
在|PQ|的最小值为d-R=
-2=
,
故选:A.
圆心到直线的距离d=
| |2×3+4×2+5| | ||
|
| 19 |
| 5 |
在|PQ|的最小值为d-R=
| 19 |
| 5 |
| 9 |
| 5 |
故选:A.
点评:本题主要考查直线和圆的位置关系的应用,求出圆心到直线的距离是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知矩形ABCD的顶点都在半径为R的球O的球面上,AB=6,BC=2
,棱锥O-ABCD的体积为8
,则球O的表面积为( )
| 3 |
| 3 |
| A、16π | B、32 |
| C、48π | D、64π |
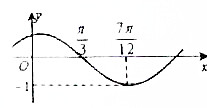 已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<