题目内容
甲、乙两个物体沿直线运动的方程分别是s1=t3-2t2+t-3，s2=3t2-t+1，则在t=3秒时两个物体运动的瞬时速度关系是（ ）
| A、乙比甲大 | B、甲比乙大 |
| C、甲乙相等 | D、甲乙无法比较 |
考点：导数的运算,变化的快慢与变化率
专题：导数的概念及应用
分析：求出位移的导函数，据位移的导数是瞬时速度；令t=3，求出物体在t=3时的瞬时速度，再比较即可
解答：
解：s1′=3t2-4t+1，s2′=6t-1，
当t=3时，
v甲=3×9-3×4+1=16，v乙=3×6-1=17，
∴v甲＜v乙
故选：A
当t=3时，
v甲=3×9-3×4+1=16，v乙=3×6-1=17，
∴v甲＜v乙
故选：A
点评：本题考查物体的位移的导数表示物体运动的瞬时速度．
练习册系列答案
相关题目
cos480°的值为（ ）
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
设i是虚数单位，则复数z=i（-2+i）的虚部为（ ）
| A、-2 | B、-1 | C、-2i | D、2i |
在△ABC中，角A、B、C所对的边分别是a、b、c，若∠C=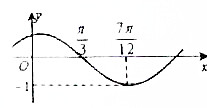
已知函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|＜