题目内容
已知tanα=2,求2sin2α-3sinαcosα-2cos2α的值.
考点:同角三角函数基本关系的运用
专题:计算题,三角函数的求值
分析:运用平方关系,将分母1化为sin2α+cos2α,再分子分母同除以cos2α,化为正切,代入数据即可得到.
解答:
解:由于tanα=2,
则2sin2α-3sinαcosα-2cos2α=
=
=
=0.
则2sin2α-3sinαcosα-2cos2α=
| 2sin2α-3sinαcosα-2cos2α |
| sin2α+cos2α |
=
| 2tan2α-3tanα-2 |
| tan2α+1 |
| 2×4-3×2-2 |
| 4+1 |
点评:本题考查同角的平方关系和商数关系,考查运算能力,属于基础题.

练习册系列答案
相关题目
已知α是第二象限角,则下列式子中值恒为正的是( )
A、sin
| ||||
B、cos
| ||||
C、tan
| ||||
D、sin
|
已知矩形ABCD的顶点都在半径为R的球O的球面上,AB=6,BC=2
,棱锥O-ABCD的体积为8
,则球O的表面积为( )
| 3 |
| 3 |
| A、16π | B、32 |
| C、48π | D、64π |
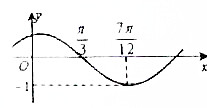 已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<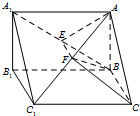 如图,在直三棱柱A1B1C1-ABC中,AB⊥BC,E、F分别是A1B,AC1的中点.
如图,在直三棱柱A1B1C1-ABC中,AB⊥BC,E、F分别是A1B,AC1的中点.