题目内容
表中显示的是某商品从4月份到10月份的价格变化统计如下:
在一次函数、二次函数、指数函数、对数函数这四个函数模型中,请确认最能代表上述变化的函数,并预测该商品11月份的价格为 元(精确到整数).
| x(月) | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y(元) | 15 | 16.9 | 19 | 20.9 | 23.1 | 25.1 | 27 |
考点:函数模型的选择与应用
专题:计算题,函数的性质及应用
分析:由题意,函数是单调增函数,且增长幅度不大.故设y=kx+b,代入(4,15),(6,19),求出函数解析式,即可得出结论.
解答:
解:由题意,函数是单调增函数,且增长幅度不大.
故设y=kx+b,则
,∴k=2,b=7,∴y=2x+7,
∴x=11时,y=29,
故答案为:29.
故设y=kx+b,则
|
∴x=11时,y=29,
故答案为:29.
点评:本题考查函数模型的选择与应用,考查学生的计算能力,比较基础.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
若各项均为正数的数列{an}满足an-1=sinan(n∈N*),则下列说法中正确的是( )
| A、{an}是单调递减数列 |
| B、{an}是单调递增数列 |
| C、{an}可能是等差数列 |
| D、{an}可能是等比数列 |
已知α是第二象限角,则下列式子中值恒为正的是( )
A、sin
| ||||
B、cos
| ||||
C、tan
| ||||
D、sin
|
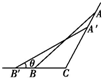 在△ABC中,角A、B、C所对的边分别是a、b、c,若∠C=
在△ABC中,角A、B、C所对的边分别是a、b、c,若∠C=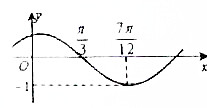 已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<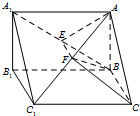 如图,在直三棱柱A1B1C1-ABC中,AB⊥BC,E、F分别是A1B,AC1的中点.
如图,在直三棱柱A1B1C1-ABC中,AB⊥BC,E、F分别是A1B,AC1的中点.