题目内容
方程e2x-kx=0有两个不相等的实数根,则实数k的取值范围为( )
A、(
| ||
B、(
| ||
| C、(e,+∞) | ||
| D、(2e,+∞) |
考点:根的存在性及根的个数判断
专题:计算题,作图题,函数的性质及应用
分析:方程e2x-kx=0有两个不相等的实数根可化为函数y=e2x与y=kx有两个不同的交点,作图找到解题关键,从而求切线时的斜率即可.
解答:
解:方程e2x-kx=0有两个不相等的实数根可化为
函数y=e2x与y=kx有两个不同的交点,
作函数y=e2x与y=kx的图象如下,

则直线l与y=e2x相切时为临界值;
设切点为(x,e2x);
则
=2e2x;
故x=
;
故k=2e;
故数k的取值范围为(2e,+∞);
故选:D.
函数y=e2x与y=kx有两个不同的交点,
作函数y=e2x与y=kx的图象如下,

则直线l与y=e2x相切时为临界值;
设切点为(x,e2x);
则
| e2x |
| x |
故x=
| 1 |
| 2 |
故k=2e;
故数k的取值范围为(2e,+∞);
故选:D.
点评:本题考查了方程的根与函数的图象的关系应用及几何意义的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设i是虚数单位,则复数z=i(-2+i)的虚部为( )
| A、-2 | B、-1 | C、-2i | D、2i |
方程2x-1-|x2-1|=-
的实根个数为( )
| 1 |
| 2 |
| A、2 |
| B、3 |
| C、4 |
| D、5 第II卷(共100分) |
若各项均为正数的数列{an}满足an-1=sinan(n∈N*),则下列说法中正确的是( )
| A、{an}是单调递减数列 |
| B、{an}是单调递增数列 |
| C、{an}可能是等差数列 |
| D、{an}可能是等比数列 |
已知α是第二象限角,则下列式子中值恒为正的是( )
A、sin
| ||||
B、cos
| ||||
C、tan
| ||||
D、sin
|
已知函数f(x)=
g(x)=x2-4x-4.设b为实数,若存在实数a,使得f(a)+g(b)=0,则实数b的取值范围是( )
|
| A、[-1,5] |
| B、(-∞,-1] |
| C、[-1,+∞) |
| D、(-∞,5] |
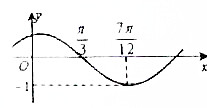 已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<