题目内容
△ABC的外接圆半径为R,∠C=60°,则
的取值范围是( )
| a+b |
| R |
A、[
| ||||
B、[
| ||||
C、(
| ||||
D、(
|
考点:正弦定理
专题:计算题,解三角形
分析:由正弦定理及和差化积公式可得:
=2
cos
,求得0≤
<
,从而有cos
∈(
,1],即可得到
的取值范围.
| a+b |
| R |
| 3 |
| A-B |
| 2 |
| A-B |
| 2 |
| π |
| 3 |
| A-B |
| 2 |
| 1 |
| 2 |
| a+b |
| R |
解答:
解:∵由正弦定理可知:a=2RsinA;b=2RsinB;
∴
=2(sinA+sinB)=2×2sin
cos
=4sin(
)cos
=2
cos
,
又∵0≤(A-B)<
;即0≤
<
;
∴cos
∈(
,1];
∴
∈(
,2
],
故选:B.
∴
| a+b |
| R |
| A+B |
| 2 |
| A-B |
| 2 |
π-
| ||
| 2 |
| A-B |
| 2 |
| 3 |
| A-B |
| 2 |
又∵0≤(A-B)<
| 2π |
| 3 |
| A-B |
| 2 |
| π |
| 3 |
∴cos
| A-B |
| 2 |
| 1 |
| 2 |
∴
| a+b |
| R |
| 3 |
| 3 |
故选:B.
点评:本题主要考查了正弦定理,和差化积公式的应用,三角函数值域的解法,综合性较强,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
已知函数f(x)=
g(x)=x2-4x-4.设b为实数,若存在实数a,使得f(a)+g(b)=0,则实数b的取值范围是( )
|
| A、[-1,5] |
| B、(-∞,-1] |
| C、[-1,+∞) |
| D、(-∞,5] |
在等差数列{an}中,若a1+a2+a8+a9=360,则数列{an}的前9项和为( )
| A、180 | B、405 |
| C、810 | D、1620 |
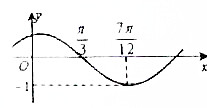 已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<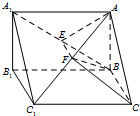 如图,在直三棱柱A1B1C1-ABC中,AB⊥BC,E、F分别是A1B,AC1的中点.
如图,在直三棱柱A1B1C1-ABC中,AB⊥BC,E、F分别是A1B,AC1的中点.