题目内容
计算：
+
（α为第四象限角）．
|
|
考点：三角函数的化简求值,同角三角函数基本关系的运用
专题：三角函数的求值
分析：根据三角函数的倍角公式进行化简即可．
解答：
解：
+
=
+
=
+
，
∵α为第四象限角，∴sinα＜0，
则
+
=-
-
=-
．
|
|
|
|
| |1-cosα| |
| |sinα| |
| |1+cosα| |
| |sinα| |
∵α为第四象限角，∴sinα＜0，
则
| |1-cosα| |
| |sinα| |
| |1+cosα| |
| |sinα| |
| 1-cosα |
| sinα |
| 1+cosα |
| sinα |
| 2 |
| sinα |
点评：本题主要考查三角函数的化简求值，根据同角的三角函数关系式是解决本题的关键．注意角的象限和三角函数符号之间的关系．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
cos480°的值为（ ）
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
在△ABC中，角A、B、C所对的边分别是a、b、c，若∠C=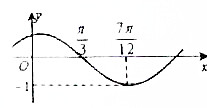
已知函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|＜
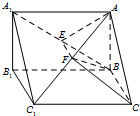如图，在直三棱柱A1B1C1-ABC中，AB⊥BC，E、F分别是A1B，AC1的中点．