题目内容
已知⊙M：x2+（y-2）2=1，Q是x轴上的动点，QA，QB分别切⊙M于A，B两点．
（1）若|AB|=
，求|MQ|、Q点的坐标以及直线MQ的方程；
（2）求证：直线AB恒过定点．
（1）若|AB|=
4
| ||
| 3 |
（2）求证：直线AB恒过定点．
考点：直线和圆的方程的应用
专题：直线与圆
分析：（1）问利用平面几何的知识，根据勾股定理、射影定理可以解决；
（2）问设点Q的坐标，由几何性质，可知A、B两点在以QM为直径的圆上，线段AB是此圆与已知圆的公共弦，即可得出结论．
（2）问设点Q的坐标，由几何性质，可知A、B两点在以QM为直径的圆上，线段AB是此圆与已知圆的公共弦，即可得出结论．
解答：
解：（1）设直线MQ交AB于点P，则|AP|=
，
又|AM|=1，AP⊥MQ，AM⊥AQ，得|MP|=
=
，
∵|MQ|=
，∴|MQ|=3．
设Q（x，0），而点M（0，2），由
=3，得x=±
，
则Q点的坐标为（
，0）或（-
，0）．
从而直线MQ的方程为2x+
y-2
=0或2x-
y+2
=0．
（2）证明：设点Q（q，0），由几何性质，
可知A、B两点在以QM为直径的圆上，此圆的方程为x（x-q）+y（y-2）=0，
而线段AB是此圆与已知圆的公共弦，
即为qx-2y+3=0，
∴直线AB恒过定点（0，
）．
| 2 |
| 3 |
| 2 |
又|AM|=1，AP⊥MQ，AM⊥AQ，得|MP|=
1-(
|
| 1 |
| 3 |
∵|MQ|=
| |MA|2 |
| |MP| |
设Q（x，0），而点M（0，2），由
| x2+22 |
| 5 |
则Q点的坐标为（
| 5 |
| 5 |
从而直线MQ的方程为2x+
| 5 |
| 5 |
| 5 |
| 5 |
（2）证明：设点Q（q，0），由几何性质，
可知A、B两点在以QM为直径的圆上，此圆的方程为x（x-q）+y（y-2）=0，
而线段AB是此圆与已知圆的公共弦，
即为qx-2y+3=0，
∴直线AB恒过定点（0，
| 3 |
| 2 |
点评：本题考查直线与圆的位置关系，考查直线恒过定点，考查平面几何的知识，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
若对于实数a、b，定义运算“*”为：a*b=
，则函数f(x)=log2x*log
x的值域为（ ）
|
| 1 |
| 2 |
| A、（0，1] |
| B、（-∞，0] |
| C、[0，+∞） |
| D、[1，+∞） |
已知函数关于x的一元二次不等式ax2-5x-50＞0的解集为（x1，x2），且x2-x1=15，则a=（ ）
| A、-1 | ||
| B、1 | ||
C、-
| ||
D、
|
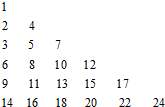把正整数按一定的规则排成了如图所示的三角形数表．设aij（i，j∈N+）是位于这个三角形数表中从上往下数第i行、从左往右数第j个数，如a42=8．若aij=2013，则i+j=