题目内容
已知f(x)=lg(x2-1).
(1)求f(x)的定义域;
(2)求使f(x)>0的x取值范围.
(1)求f(x)的定义域;
(2)求使f(x)>0的x取值范围.
考点:指、对数不等式的解法,函数的定义域及其求法,对数函数的定义域
专题:函数的性质及应用
分析:(1)根据对数函数成立的条件建立不等式即可求函数的定义域.
(2)直接根据对数不等式的解法解不等式即可.
(2)直接根据对数不等式的解法解不等式即可.
解答:
解:(1)令x2-1>0,解得x<-1或x>1.
所以f(x)的定义域的定义域为(-∞,1)∪(1,+∞).
(2)因为y=lgt为(0,+∞)上的增函数,
所以由f(x)>0得x2-1>1,即x2>2,
解得x<-
或x>
.
于是使f(x)>0的x取值范围是(-∞,-
)∪(
,+∞).
所以f(x)的定义域的定义域为(-∞,1)∪(1,+∞).
(2)因为y=lgt为(0,+∞)上的增函数,
所以由f(x)>0得x2-1>1,即x2>2,
解得x<-
| 2 |
| 2 |
于是使f(x)>0的x取值范围是(-∞,-
| 2 |
| 2 |
点评:本题主要考查对数函数的图象和性质,要求熟练掌握对数函数的性质,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一个几何体的三视图如图所示,则该几何体的体积为( )


| A、12-π | B、12-2π |
| C、6-π | D、4-π |
实数x,y满足
,则z=x-3y的最小值为( )
|
| A、4 | B、-2 | C、-8 | D、-10 |
在一个棱长为3cm的正方体的表面涂上颜色,将其适当分割成棱长为1cm的小正方体,全部放入不透明的口袋中,搅拌均匀后,从中任取一个,取出的小正方体表面仅有一个面涂有颜色的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知x、y满足约束条件
,则z=3x+5y的最小值为( )
|
| A、17 | B、-11 |
| C、11 | D、-17 |
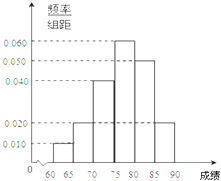 在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,为调查其测试前的培训辅导情况与测试成绩的相关性,抽取每个考室中座位号为05的考生,统计了他们的成绩,得到如图所示的频率分布直方图.
在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,为调查其测试前的培训辅导情况与测试成绩的相关性,抽取每个考室中座位号为05的考生,统计了他们的成绩,得到如图所示的频率分布直方图.