题目内容
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
如图所示.
(1)试确定f(x)的解析式;
(2)若x∈[0,1],求函数f(x)的值域.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的定义域和值域
专题:计算题,三角函数的图像与性质
分析:(1)由f(x)=Asin(ωx+φ)的部分图象知A=2,易求其周期T=2,从而可得ω,将点P(
,2)代入y=2sin(πx+φ)可求φ,从而可得f(x)的解析式;
(2)x∈[0,1]⇒πx+
∈[
,
],利用正弦函数的单调性即可求得f(x)的值域.
| 1 |
| 3 |
(2)x∈[0,1]⇒πx+
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
解答:
解:(1)由图象可知A=2,且
=
-
=
,
∴T=2,即ω=
=π,
将点P(
,2)代入y=2sin(πx+φ)得sin(
+φ)=1,
又|φ|≤
,
∴φ=
.
故所求解析式为f(x)=2sin(πx+
).
(Ⅱ)∵x∈[0,1]
∴πx+
∈[
,
],
∴-
≤sin(πx+
)≤1,
∴f(x)的值域为[-1,2].
| T |
| 4 |
| 5 |
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
∴T=2,即ω=
| 2π |
| T |
将点P(
| 1 |
| 3 |
| π |
| 3 |
又|φ|≤
| π |
| 2 |
∴φ=
| π |
| 6 |
故所求解析式为f(x)=2sin(πx+
| π |
| 6 |
(Ⅱ)∵x∈[0,1]
∴πx+
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
∴-
| 1 |
| 2 |
| π |
| 6 |
∴f(x)的值域为[-1,2].
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查正弦函数的单调性,属于中档题.

练习册系列答案
相关题目
若点(a,-1)在函数y=log
x的图象上,则tan
的值为( )
| 1 |
| 2 |
| aπ |
| 6 |
| A、0 | ||||
B、
| ||||
| C、1 | ||||
D、
|
已知函数f(x)=|x2-6|,若a<b<0,且f(a)=f(b),则a2b的最小值是( )
| A、-16 | B、-12 |
| C、-10 | D、-8 |
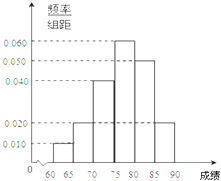 在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,为调查其测试前的培训辅导情况与测试成绩的相关性,抽取每个考室中座位号为05的考生,统计了他们的成绩,得到如图所示的频率分布直方图.
在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,为调查其测试前的培训辅导情况与测试成绩的相关性,抽取每个考室中座位号为05的考生,统计了他们的成绩,得到如图所示的频率分布直方图.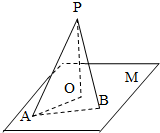 如图,直线PO⊥平面M,垂足为O,直线PA是平面M的一条斜线,斜足为A,其中∠APO=α,过点P的动直线PB交平面M于点B,∠APB=β,则下列说法正确的是
如图,直线PO⊥平面M,垂足为O,直线PA是平面M的一条斜线,斜足为A,其中∠APO=α,过点P的动直线PB交平面M于点B,∠APB=β,则下列说法正确的是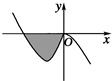 (1)
(1)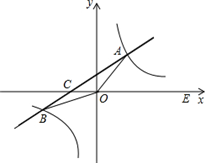 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=