题目内容
已知双曲线的左右焦点F1,F2的坐标为(-4,0)与(4,0),离心率e=2.
(1)求双曲线的方程;
(2)已知椭圆
+
=1,点P是双曲线与椭圆两曲线在第一象限的交点,求|PF1|•|PF2|的值.
(1)求双曲线的方程;
(2)已知椭圆
| x2 |
| 36 |
| y2 |
| 20 |
考点:圆锥曲线的综合
专题:圆锥曲线的定义、性质与方程
分析:(1)由双曲线的焦点坐标及离心率,可求得实半轴长,再由b2=c2-a2求得虚半轴,则双曲线方程可求;
(2)由椭圆方程求得椭圆焦点与双曲线焦点重合,利用椭圆及双曲线定义列式求出P到两个焦点的距离,则答案可求.
(2)由椭圆方程求得椭圆焦点与双曲线焦点重合,利用椭圆及双曲线定义列式求出P到两个焦点的距离,则答案可求.
解答:
解:(1)∵c=4,e=
=2,
∴a=2,则b2=c2-a2=12,
∴双曲线的方程为:
-
=1;
(2)由椭圆
+
=1,知其左右焦点为F1(-4,0)与F2(4,0),
又点P是双曲线与椭圆两曲线在第一象限的交点,由椭圆及双曲线定义得:
,
则|PF1|=8,|PF2|=4,
∴|PF1|•|PF2|=32.
| c |
| a |
∴a=2,则b2=c2-a2=12,
∴双曲线的方程为:
| x2 |
| 4 |
| y2 |
| 12 |
(2)由椭圆
| x2 |
| 36 |
| y2 |
| 20 |
又点P是双曲线与椭圆两曲线在第一象限的交点,由椭圆及双曲线定义得:
|
则|PF1|=8,|PF2|=4,
∴|PF1|•|PF2|=32.
点评:本题考查了圆锥曲线的综合题,解答的关键是利用圆锥曲线的定义列式,求出P点到两焦点的距离后得答案,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知x0是函数f(x)=(
)x-
的一个零点,若x1∈(0,x0),x2∈(x0,+∞),则( )
| 1 |
| 2 |
| x |
| A、f(x1)<0,f(x2)<0 |
| B、f(x1)>0,f(x2)<0 |
| C、f(x1)<0,f(x2)>0 |
| D、f(x1)>0,f(x2)>0 |
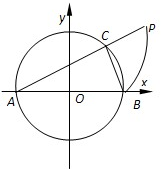 如图,在直角坐标系xoy中,AB是半圆O:x2+y2=1(y≥0)的直径,点C是半圆O上任一点,延长AC到点P,使CP=CB,当点C从点B运动到点A时,动点P的轨迹的长度是( )
如图,在直角坐标系xoy中,AB是半圆O:x2+y2=1(y≥0)的直径,点C是半圆O上任一点,延长AC到点P,使CP=CB,当点C从点B运动到点A时,动点P的轨迹的长度是( )| A、2π | ||
B、
| ||
| C、π | ||
D、4
|
已知曲线C:x2+y2-2x+2y=0与直线L:y+2=k(x-2),则C与L的公共点( )
| A、有2个 | B、最多1个 |
| C、至少1个 | D、不存在 |
 在边长为10的正方形ABCD内有一动点P,AP=9,作PQ⊥BC于Q,PR⊥CD于R,求矩形PQCR面积的最小值和最大值,并指出取最大值时P的具体位置.
在边长为10的正方形ABCD内有一动点P,AP=9,作PQ⊥BC于Q,PR⊥CD于R,求矩形PQCR面积的最小值和最大值,并指出取最大值时P的具体位置.