题目内容
已知x0是函数f(x)=(
)x-
的一个零点,若x1∈(0,x0),x2∈(x0,+∞),则( )
| 1 |
| 2 |
| x |
| A、f(x1)<0,f(x2)<0 |
| B、f(x1)>0,f(x2)<0 |
| C、f(x1)<0,f(x2)>0 |
| D、f(x1)>0,f(x2)>0 |
考点:函数的零点与方程根的关系
专题:函数的性质及应用
分析:因为x0是函数f(x)=(
)x-
的一个零点,可得到f(x0)=0,再由函数f(x)的单调性可得到答案.
| 1 |
| 2 |
| x |
解答:
解:∵x0是f(x)=(
)x-
的一个零点,
∴f(x0)=0
∵f(x)=(
)x-
是单调递减函数,且x1∈(0,x0),x2∈(x0,+∞),
∴f(x1)>f(x0)=0>f(x2),
故选B.
| 1 |
| 2 |
| x |
∴f(x0)=0
∵f(x)=(
| 1 |
| 2 |
| x |
∴f(x1)>f(x0)=0>f(x2),
故选B.
点评:本题考查了函数零点的概念和函数单调性的问题,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设函数f(x)=
(a∈R).若方程f(f(x))=x有解,则a的取值范围为( )
| x-a |
A、(-∞,
| ||
B、(0,
| ||
C、(-∞,
| ||
| D、[1,+∞) |
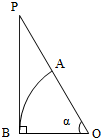 如图,直角△POB中,∠PBO=90°,以O为圆心、OB为半径作圆弧交OP于A点.若圆弧
如图,直角△POB中,∠PBO=90°,以O为圆心、OB为半径作圆弧交OP于A点.若圆弧
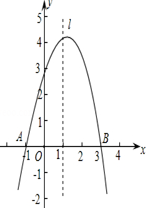 已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.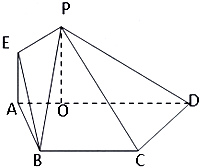 如图,在等腰梯形ABCD中,AD∥BC,
如图,在等腰梯形ABCD中,AD∥BC,