题目内容
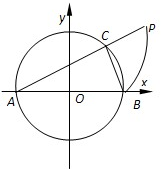 如图,在直角坐标系xoy中,AB是半圆O:x2+y2=1(y≥0)的直径,点C是半圆O上任一点,延长AC到点P,使CP=CB,当点C从点B运动到点A时,动点P的轨迹的长度是( )
如图,在直角坐标系xoy中,AB是半圆O:x2+y2=1(y≥0)的直径,点C是半圆O上任一点,延长AC到点P,使CP=CB,当点C从点B运动到点A时,动点P的轨迹的长度是( )| A、2π | ||
B、
| ||
| C、π | ||
D、4
|
考点:轨迹方程
专题:计算题,直线与圆
分析:根据题意,△BCP是以C为直角顶点的等腰直角三角形,可得直线PA到PB的角为45°.由此P(x,y),利用直线的斜率公式建立关于x、y的关系式,化简得到x2+(y-1)2=2,进而利用圆的周长公式算出点P的轨迹的长度.
解答:
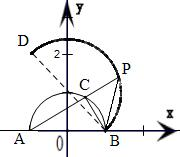 解:连结BP,根据题意可得△BCP是以C为直角顶点的等腰直角三角形.
解:连结BP,根据题意可得△BCP是以C为直角顶点的等腰直角三角形.
∴∠APB=45°,即直线PA到PB的角为45°,
设P(x,y),可得kPA=
,kPB=
,
∴tan45°=
=1,
化简得x2+(y-1)2=2.
∴点P的轨迹方程为x2+(y-1)2=2,
由已知y≥0可得kPA=
>0,
可知P点的轨迹是以(0,1)为圆心、半径r=
的半圆,
可得轨迹的长度是
×2πr=
π.
故选:B
 解:连结BP,根据题意可得△BCP是以C为直角顶点的等腰直角三角形.
解:连结BP,根据题意可得△BCP是以C为直角顶点的等腰直角三角形.∴∠APB=45°,即直线PA到PB的角为45°,
设P(x,y),可得kPA=
| y |
| x+1 |
| y |
| x-1 |
∴tan45°=
| ||||
1+
|
化简得x2+(y-1)2=2.
∴点P的轨迹方程为x2+(y-1)2=2,
由已知y≥0可得kPA=
| y |
| x+1 |
可知P点的轨迹是以(0,1)为圆心、半径r=
| 2 |
可得轨迹的长度是
| 1 |
| 2 |
| 2 |
故选:B
点评:本题给出动点满足的条件,求动点的轨迹形成图形的长度.着重考查了圆的性质、直线的斜率公式和动点的轨迹及其应用等知识,属于中档题.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
在样本的频率分布直方图中,共有11个小长方形,若中间一个小长方形的面积等于其他10个小长方形的面积的和的
,且样本容量为200,则中间一组有频数为( )
| 1 |
| 4 |
| A、40 | B、32 |
| C、0.2 | D、0.25 |
cos(-
)的值等于( )
| 5π |
| 3 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
在面积为1的正方形ABCD内部随机取一点P,则△PAB的面积大于等于
的概率是( )
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
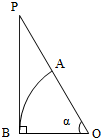 如图,直角△POB中,∠PBO=90°,以O为圆心、OB为半径作圆弧交OP于A点.若圆弧
如图,直角△POB中,∠PBO=90°,以O为圆心、OB为半径作圆弧交OP于A点.若圆弧
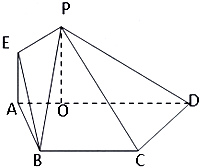 如图,在等腰梯形ABCD中,AD∥BC,
如图,在等腰梯形ABCD中,AD∥BC,