题目内容
体积为52的圆台,一个底面积是另一个底面积的9倍,那么截得这个圆台的圆锥的体积是 .
考点:组合几何体的面积、体积问题
专题:计算题
分析:将圆台补成如图所示的圆锥,利用几何体的相似比与面积比、体积比的关系,可得大圆锥的体积和圆台体积之比,即可得出答案.
解答:
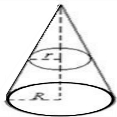 解:如图所示,将圆台补成圆锥,则图中小圆锥与大圆锥是相似的几何体
解:如图所示,将圆台补成圆锥,则图中小圆锥与大圆锥是相似的几何体
设大、小圆锥的底面半径分别为r、R,高分别为h、H
∵圆台上、下底面的面积之比为1:9,
∴小圆锥与大圆锥的相似比为1:3,即半径之比
=
且高之比
=
因此,小圆锥与大圆锥的体积之比
=(
)3=
,
可得
=1-
=
,
因此,截得这个圆台的圆锥体积和圆台体积之比27:26,
又圆台的体积为52cm3,则截该圆台的圆锥体积为
×52=54.
故答案为:54.
 解:如图所示,将圆台补成圆锥,则图中小圆锥与大圆锥是相似的几何体
解:如图所示,将圆台补成圆锥,则图中小圆锥与大圆锥是相似的几何体设大、小圆锥的底面半径分别为r、R,高分别为h、H
∵圆台上、下底面的面积之比为1:9,
∴小圆锥与大圆锥的相似比为1:3,即半径之比
| r |
| R |
| 1 |
| 3 |
| h |
| H |
| 1 |
| 3 |
因此,小圆锥与大圆锥的体积之比
| V小 |
| V大 |
| 1 |
| 3 |
| 1 |
| 27 |
可得
| V圆台 |
| V大 |
| 1 |
| 27 |
| 26 |
| 27 |
因此,截得这个圆台的圆锥体积和圆台体积之比27:26,
又圆台的体积为52cm3,则截该圆台的圆锥体积为
| 27 |
| 26 |
故答案为:54.
点评:本题考查几何体的体积的求法,通过圆台的上下底面面积之比,求截得这个圆台的圆锥体积和圆台体积之比.着重考查了锥体体积计算公式和相似几何体的性质等知识.

练习册系列答案
相关题目
在样本的频率分布直方图中,共有11个小长方形,若中间一个小长方形的面积等于其他10个小长方形的面积的和的
,且样本容量为200,则中间一组有频数为( )
| 1 |
| 4 |
| A、40 | B、32 |
| C、0.2 | D、0.25 |
在面积为1的正方形ABCD内部随机取一点P,则△PAB的面积大于等于
的概率是( )
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.