Question

在边长为10的正方形ABCD内有一动点P，AP=9，作PQ⊥BC于Q，PR⊥CD于R，求矩形PQCR面积的最小值和最大值，并指出取最大值时P的具体位置．

Answer 1

考点：三角函数的最值

专题：计算题

分析：连结AP，延长RP交AB于H，设∠HAP=θ，把矩形PQCR的面积用含θ的代数式表示，换元后利用配方法求函数的最值．

解答： 解：如图，
θ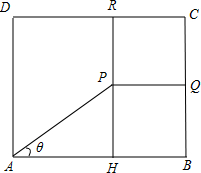
连结AP，延长RP交AB于H，设∠HAP=θ，则PH=9sinθ，AH=9cosθ，
设矩形PQCR的面积为y，
则y=PR•PQ=（10-9sinθ）（10-9cosθ）=100-90（sinθ+cosθ）+81sinθcosθ．
设sinθ+cosθ=t，
则sinθcosθ=

t2-1

2

，
又t=

2

sin(θ+

π

4

)，θ∈(0， 

π

2

)，
∴1＜t≤

2

，
∴y=

81t2

2

-90t+

119

2

=

81

2

(t-

10

9

)2+

19

2

（1＜t≤

2

）．
∵

10

9

∈(1， 

2

]，
∴当t=

10

9

时，ymin=

19

2

．
当t=

2

时，ymax=

281-180 2

2

．
此时，

2

sin(θ+

π

4

)=

2

，
又

π

4

＜θ+

π

4

＜

3π

4

，∴θ=

π

4

．

点评：本题考查了三角函数的最值，考查了数形结合的解题思想方法，解答的关键是把矩形PQCR面积表示为一个角的函数，是中档题．