题目内容
p≤2是数列an=n2-pn为递增数列的 条件．
考点：必要条件、充分条件与充要条件的判断
专题：点列、递归数列与数学归纳法
分析：首先，写出an+1=（n+1）2-p（n+1），然后，作差，进行化简，得到p＜1+2n，然后，再根据n的取值进行求解范围即可．
解答：
解：∵an=n2-pn，
∴an+1=（n+1）2-p（n+1），
=n2+（2-p）n+1-p，
∵数列an=n2-pn为递增数列，
∴an+1-an＞0，
∴n2+（2-p）n+1-p-n2+pn＞0，
∴2n+1-p＞0．
∴p＜1+2n，
∵n为正整数，
∴p＜3，
∴p≤2是数列an=n2-pn为递增数列的充分不必要条件，
故答案为：充分不必要．
∴an+1=（n+1）2-p（n+1），
=n2+（2-p）n+1-p，
∵数列an=n2-pn为递增数列，
∴an+1-an＞0，
∴n2+（2-p）n+1-p-n2+pn＞0，
∴2n+1-p＞0．
∴p＜1+2n，
∵n为正整数，
∴p＜3，
∴p≤2是数列an=n2-pn为递增数列的充分不必要条件，
故答案为：充分不必要．
点评：本题重点考查了数列的单调性、充分条件和必要条件及其判断方法等知识，属于中档题．
练习册系列答案
相关题目
读如图程序，当输出的值y的范围大于1时，则输入的x值的取值范围是（ ）
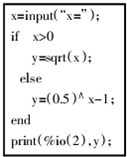
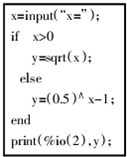
| A、（-∞，-1） |
| B、（1，+∞） |
| C、（-∞，-1）∪（1，+∞） |
| D、（-∞，0）∪（0，+∞） |
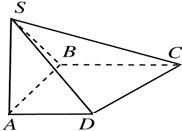如图所示，ABCD是直角梯形，∠ABC=90°，SA⊥底面ABCD，SA=AB=BC=1，AD=
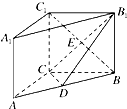如图，在直三棱柱ABC-A1B1C1中，AC=3，BC=4，AB=5，点D是线段AB上的一点，且∠CDB1=90°，AA1=CD，则点A1到平面B1CD的距离为
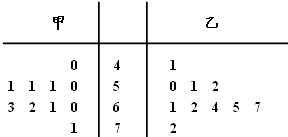随机抽取某中学甲、乙两班各10名学生，测量他们的体重（单位：kg），获得体重数据的茎叶图如图：