题目内容
已知O为原点,A(x1,y1),B(x2,y2)是椭圆C:
+
=1(0<m<4)上任意两点,向量
=(x1,
),
=(x2,
)且
⊥
,椭圆的离心率e=
,求△AOB的面积是否为定值?
| x2 |
| m |
| y2 |
| 4 |
| p |
| y1 |
| 2 |
| q |
| y2 |
| 2 |
| p |
| q |
| ||
| 2 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知条件推导出a=2,且
=
,由此能求出椭圆C的标准方程.
(2)由已知条件推导出x1x2+
=0,设直线AB方程为:y=kx+m,联立x2+
=1,得(4+k2)x2+2kmx+m2-4=0,由此利用韦达定理结合已知条件能求出三角形AOB的面积为定值1.
| c |
| a |
| ||
| 2 |
(2)由已知条件推导出x1x2+
| y1y2 |
| 4 |
| y2 |
| 4 |
解答:
解:(1)∵椭圆C:
+
=1(0<m<4)的离心率e=
,
∴a=2,且
=
,
解得a=2,c=
,m=1,
∴椭圆C的标准方程为x2+
=1.(5分)
(2)∵A(x1,y1),B(x2,y2)
是椭圆C:
+
=1(0<m<4)上任意两点,
向量
=(x1,
),
=(x2,
)且
⊥
,
∴x1x2+
=0,(6分)
当直线AB斜率存在时,
设直线AB方程为:y=kx+m,联立x2+
=1,
消去y得(4+k2)x2+2kmx+m2-4=0,
∴△=4k2m2-4(4+k2)(m2-4)>0,
x1+x2=-
,x1x2=
,
∴4x1x2+y1y2=4x1x2+(kx1+m)(kx2+m)
=(4+k2)x1x2+km(x1+x2)+m2=0,
即(4+k2)(
)+(km)(-
)+m2=0,
化简得2m2-k2-4=0,(8分)
S△ADB=
|-
|•|y1-y2|
=
|m||x1-x2|
=
|m|
=
|m|
=
|m|
=
|m|
=
|m|
=
|m|
=1.(10分)
当直线AB斜率不存在时,
设直线AB方程为:x=t,(-1<t<1),
联立椭圆x2+
=1,解得y=±2
,
不妨设A(t,2
),B(t,-2
),
代入4x1x2+y1y2=0,得t2=
,t=±
,
此时S△ADE=
•
•2
=1,
综上,三角形AOB的面积为定值1.(12分)
| x2 |
| m |
| y2 |
| 4 |
| ||
| 2 |
∴a=2,且
| c |
| a |
| ||
| 2 |
解得a=2,c=
| 3 |
∴椭圆C的标准方程为x2+
| y2 |
| 4 |
(2)∵A(x1,y1),B(x2,y2)
是椭圆C:
| x2 |
| m |
| y2 |
| 4 |
向量
| p |
| y1 |
| 2 |
| q |
| y2 |
| 2 |
| p |
| q |
∴x1x2+
| y1y2 |
| 4 |
当直线AB斜率存在时,
设直线AB方程为:y=kx+m,联立x2+
| y2 |
| 4 |
消去y得(4+k2)x2+2kmx+m2-4=0,
∴△=4k2m2-4(4+k2)(m2-4)>0,
x1+x2=-
| 2km |
| 4+k2 |
| m2-4 |
| 4+k2 |
∴4x1x2+y1y2=4x1x2+(kx1+m)(kx2+m)
=(4+k2)x1x2+km(x1+x2)+m2=0,
即(4+k2)(
| m2-4 |
| 4+k2 |
| 2km |
| 4+k2 |
化简得2m2-k2-4=0,(8分)
S△ADB=
| 1 |
| 2 |
| m |
| k |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
| (x1+x2)2-4x1x2 |
=
| 1 |
| 2 |
(-
|
=
| 1 |
| 2 |
|
=
| 1 |
| 2 |
|
=
| 1 |
| 2 |
4
| ||
| 4+k2 |
=
| 1 |
| 2 |
4
| ||
| 2m2 |
当直线AB斜率不存在时,
设直线AB方程为:x=t,(-1<t<1),
联立椭圆x2+
| y2 |
| 4 |
| 1-t2 |
不妨设A(t,2
| 1-t2 |
| 1-t2 |
代入4x1x2+y1y2=0,得t2=
| 1 |
| 2 |
| ||
| 2 |
此时S△ADE=
| 1 |
| 2 |
| ||
| 2 |
| 2 |
综上,三角形AOB的面积为定值1.(12分)
点评:本题考查椭圆标准方程的求法,考查三角形面积是否为定值的判断与求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
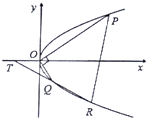 如图,已知抛物线y2=x,过原点O作两条相互垂直的直线,分别交抛物线于点P,Q
如图,已知抛物线y2=x,过原点O作两条相互垂直的直线,分别交抛物线于点P,Q 某同学为了研究函数f(x)=
某同学为了研究函数f(x)=