题目内容
已知函数f(x)=klnx,g(x)=ex.
(1)若函数φ(x)=f(x)+x-
,求φ(x)的单调区间;
(2)设直线l为函数f(x)的图象上一点A(x0,f(x0))处的切线.若在区间(2,+∞)上存在唯一的x0,使得直线l与曲线y=g(x)相切,求实数k的取值范围.
(1)若函数φ(x)=f(x)+x-
| 2 |
| x |
(2)设直线l为函数f(x)的图象上一点A(x0,f(x0))处的切线.若在区间(2,+∞)上存在唯一的x0,使得直线l与曲线y=g(x)相切,求实数k的取值范围.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)把f(x)的解析式代入φ(x)=f(x)+x-
,求导后得到φ′(x)=
,然后利用分子二次三项式对应方程的判别式与0的关系得到k的范围,由k得范围及二次三项式在不同区间内的符号得到导函数的符号,进一步得到定义域内φ(x)的单调区间;
(2)利用导数求出过f(x)的图象上一点A(x0,f(x0))处的切线l的方程,再设出l与g(x)的切点B的坐标,由导数得到l的另一方程,通过比较系数得到两切点横坐标间的关系,进一步得到k与A点横坐标的关系lnk=1+x0+lnx0-x0lnx0,构造辅助函数h(x)=1+x+lnx-xlnx(x>2),利用导数判断其单调性,求出其最值,列不等式求得在区间(2,+∞)上存在唯一的x0,使得直线l与曲线y=g(x)相切的实数k的取值范围.
| 2 |
| x |
| x2+kx+2 |
| x2 |
(2)利用导数求出过f(x)的图象上一点A(x0,f(x0))处的切线l的方程,再设出l与g(x)的切点B的坐标,由导数得到l的另一方程,通过比较系数得到两切点横坐标间的关系,进一步得到k与A点横坐标的关系lnk=1+x0+lnx0-x0lnx0,构造辅助函数h(x)=1+x+lnx-xlnx(x>2),利用导数判断其单调性,求出其最值,列不等式求得在区间(2,+∞)上存在唯一的x0,使得直线l与曲线y=g(x)相切的实数k的取值范围.
解答:
解:(1)∵f(x)=klnx,
∴f(x)+x-
=klnx+x-
(x>0),
φ′(x)=
+1+
=
,
方程x2+kx+2=0的判别式△=k2-8.
由△>0,得k<-2
或k>2
.
当△>0时,x1=
,x2=
.
若k>2
,φ′(x)>0在x∈(0,+∞)上恒成立,
若k<-2
,当x∈(0,x1),(x2,+∞)时,φ′(x)>0.
当x∈(x1,x2)时,φ′(x)<0.
若-2
≤k≤2
,φ′(x)>0在x∈(0,+∞)上恒成立.
∴若k<-2
,函数φ(x)的增区间为(0,x1),(x2,+∞),减区间为(x1,x2);
若k≥-2
,则函数φ(x)的增区间为(0,+∞).
(2)由f(x)=klnx,得f′(x)=
,f′(x0)=
.
∴直线l的方程为y-klnx0=
(x-x0),即y=
x+klnx0-k.
设l与y=g(x)切于点B(x1,y1),
则l的方程又可写为y-ex1=ex1(x-x1),即y=ex1x+ex1(1-x1).
∴
⇒k(lnx0-1)=
(1-x1)⇒x0(lnx0-1)=1-x1
⇒x1=1+x0-x0lnx0,
又x1=ln
,
化简得:lnk=1+x0+lnx0-x0lnx0.
设h(x)=1+x+lnx-xlnx(x>2),h′(x)=1+
-(lnx+1)=
-lnx,
当x>2时,
<lnx,
∴h′(x)<0恒成立,h(x)在(2,+∞)上单调递减,
且h(2)=3-ln2,要使x0唯一,只要令lnk<3-ln2=ln
.
∴0<k<
.
∴实数k的取值范围是(0,
).
∴f(x)+x-
| 2 |
| x |
| 2 |
| x |
φ′(x)=
| k |
| x |
| 2 |
| x2 |
| x2+kx+2 |
| x2 |
方程x2+kx+2=0的判别式△=k2-8.
由△>0,得k<-2
| 2 |
| 2 |
当△>0时,x1=
-k-
| ||
| 2 |
-k+
| ||
| 2 |
若k>2
| 2 |
若k<-2
| 2 |
当x∈(x1,x2)时,φ′(x)<0.
若-2
| 2 |
| 2 |
∴若k<-2
| 2 |
若k≥-2
| 2 |
(2)由f(x)=klnx,得f′(x)=
| k |
| x |
| k |
| x0 |
∴直线l的方程为y-klnx0=
| k |
| x0 |
| k |
| x0 |
设l与y=g(x)切于点B(x1,y1),
则l的方程又可写为y-ex1=ex1(x-x1),即y=ex1x+ex1(1-x1).
∴
|
| k |
| x0 |
⇒x1=1+x0-x0lnx0,
又x1=ln
| k |
| x0 |
化简得:lnk=1+x0+lnx0-x0lnx0.
设h(x)=1+x+lnx-xlnx(x>2),h′(x)=1+
| 1 |
| x |
| 1 |
| x |
当x>2时,
| 1 |
| x |
∴h′(x)<0恒成立,h(x)在(2,+∞)上单调递减,
且h(2)=3-ln2,要使x0唯一,只要令lnk<3-ln2=ln
| e3 |
| 2 |
∴0<k<
| e3 |
| 2 |
∴实数k的取值范围是(0,
| e3 |
| 2 |
点评:本题考查了利用导数研究曲线上某点处的切线方程,考查了利用导数研究函数的单调性,考查了数学转化思想方法,训练了利用导数求函数的最值,综合考查了学生分析问题和解决问题的能力,是压轴题.

练习册系列答案
相关题目
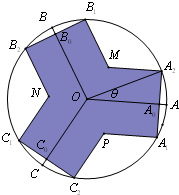 如图,半径为1的圆O,∠AOB=∠BOC=∠COA=
如图,半径为1的圆O,∠AOB=∠BOC=∠COA=