已知等差数列{an}的前10项和S10=-40.前9项和S9=-27．(Ⅰ)求数列{an}的通项公式,(Ⅱ)设bn=an+2n.求数列{bn}的前n项和Tn．题目和参考答案——青夏教育精英家教网—

题目内容

已知等差数列{a_n}的前10项和S₁₀=-40，前9项和S₉=-27．
（Ⅰ）求数列{a_n}的通项公式；
（Ⅱ）设b_n=a_n+2ⁿ，求数列{b_n}的前n项和T_n．

考点：数列的求和,等差数列的通项公式

专题：

分析：（Ⅰ）求数列{a_n}的通项公式；
（Ⅱ）求出b_n=a_n+2ⁿ，利用分组求和法，即可求数列{b_n}的前n项和T_n．

解答： 解：（Ⅰ）∵等差数列{a_n}的前10项和S₁₀=-40，前9项和S₉=-27，
∴

9a1+

9×8

d=-27

10a1+

10×9

d=-40

，解得a₁=5，d=-2，
则数列{a_n}的通项公式a_n=5-2（n-1）=7-2n；
（Ⅱ）∵b_n=a_n+2ⁿ=7-2n+2ⁿ，
∴数列{b_n}的前n项和T_n=na1+

n(n-1)

2(1-2n)

1-2

=5n-n（n-1）+2ⁿ⁺¹-2=2ⁿ⁺¹+6n+n²-2．

点评：本题主要考查等差数列的通项公式以及利用分组法进行求等差数列和等比数列的前n项和．

练习册系列答案

相关题目

），且被圆C：x²+y²=25截得的弦长等于8的直线方程．

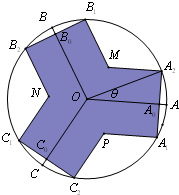如图，半径为1的圆O，∠AOB=∠BOC=∠COA=

2π

，点A₀，B₀，C₀分别是半径OA、OB、CO上的动点，且OA₀=OB₀=OC₀，分别过A₀，B₀，C₀作半径OA、OB、CO的垂线，交圆O与A₁，A₂，B₁，B₂，C₁，C₂，过A₂，B₁分别作OA、OB的平行线A₂M和B₁M交于点M，过B₂，C₁分别作OB、OC的平行线B₂N和C₁N交于点N，过C₂，A₁分别作OC、OA的平行线C₂P和A₁P交于点P，由A₁A₂MB₁B₂NC₁C₂P围成图所示的平面区域（阴影部分），记它的面积为y，设∠A₂OA=θ，用y=f（θ）表示y关于θ的函数．
（1）设θ∈（0，

]，求y=f（θ）的解析式；
（2）在（1）的条件下，求y=f（θ）的最大值，并求出当函数取最大值是时tan2θ的值．

已知O为原点，A（x₁，y₁），B（x₂，y₂）是椭圆C：

）²+y²=16相内切．
（Ⅰ）求动圆的圆心P的轨迹方程；
（Ⅱ）已知点A（2，0），点B（1，0），过点B且斜率为k₁（k₁≠0）的直线l与（Ⅰ）中的轨迹相交于C、D两点，直线AC、AD分别交直线x=3于E、F两点，线段EF的中点为Q．记直线QB的斜率为k₂，求证：k₁•k₂为定值．

=1于A、B两点，若点M（2，1）恰好为线段AB的中点，求直线L的斜率．

已知直线l：x-

y+1=0，一个圆的圆心C在x轴正半轴上，且该圆与直线l和y轴均相切．
（1）求该圆的方程；
（2）若直线：mx+y+

m=0与圆C交于A，B两点，且|AB|=

，求m的值．

如图，将边长为1的正方形ABCD沿对角线AC折起，使得平面ADC⊥平面ABC，在折起后形成的三棱锥D-ABC中，给出下列三个命题：
①△DBC是等边三角形；
②AC⊥BD；
③三棱锥D-ABC的体积是

；
④AB与CD所成的角是60°．
其中正确命题的序号是

．（写出所有正确命题的序号）

已知函数f（x）=|x²-8|，若a≤b≤0，且f（a）=f（b），则a+b的最小值是

．

试题分类