题目内容
已知椭圆
+
=1(a>b>0)的短半轴长为1,点M(2,t)(t>0)是右准线x=
上的动点.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设F为椭圆的右焦点,过F作OM的垂线与以OM为直径的圆交于点N,求ON的长.
(Ⅲ)求以OM为直径且被直线3x-4y-5=0截得的弦长为2的圆的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| c |
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设F为椭圆的右焦点,过F作OM的垂线与以OM为直径的圆交于点N,求ON的长.
(Ⅲ)求以OM为直径且被直线3x-4y-5=0截得的弦长为2的圆的方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已和条件推导出b=1,
=2,由此能求出椭圆方程.
(Ⅱ)由(Ⅰ)知F(1,0),依题意FN⊥OM,MN⊥ON,设N(x0,y0),由FN⊥OM,得2x0+ty0=2,由MN⊥ON,x02+y02=2x0+ty0=2,由此能求出|ON|.
(Ⅲ)以OM为直径的圆的圆心为(1,
),半径为r=
,由已知条件推导出
+1=
+1,由此能求出圆的方程.
| a2 |
| c |
(Ⅱ)由(Ⅰ)知F(1,0),依题意FN⊥OM,MN⊥ON,设N(x0,y0),由FN⊥OM,得2x0+ty0=2,由MN⊥ON,x02+y02=2x0+ty0=2,由此能求出|ON|.
(Ⅲ)以OM为直径的圆的圆心为(1,
| t |
| 2 |
1+
|
| t2 |
| 4 |
| 4(t+1)2 |
| 25 |
解答:
解:(Ⅰ)∵椭圆
+
=1(a>b>0)的短半轴长为1,
∴b=1,
∵点M(2,t)(t>0)是右准线x=
上的动点,
∴
=2,
∴
=
=2,解得c=1,a2=2,
∴椭圆方程为
+y2=1.
(Ⅱ)由(Ⅰ)知F(1,0),
依题意FN⊥OM,MN⊥ON,
设N(x0,y0),则
=(x0-1,y0),
=(2,t),
=(x0-2,y0-t),
=(x0,y0),
则
=(x0-1,y0),
=(2,t),
=(x0-2,y0-t),
=(x0,y0),
由FN⊥OM,得2(x0-1)+ty0=0,
∴2x0+ty0=2,
由MN⊥ON,得x0(x0-2)+y0(y0-t)=0,
∴x02+y02=2x0+ty0=2,
∴|ON|=
=
.
(Ⅲ)以OM为直径的圆的圆心为(1,
),半径为r=
,
圆心(1,
)到直线3x-4y-5=0的距离为d=
,
又圆被直线3x-4y-5=0截得的弦长为2,
∴r2=d2+1,∴
+1=
+1,解得t=4,
∴圆的方程为(x-1)2+(y-2)2=5.
| x2 |
| a2 |
| y2 |
| b2 |
∴b=1,
∵点M(2,t)(t>0)是右准线x=
| a2 |
| c |
∴
| a2 |
| c |
∴
| b2+c2 |
| c |
| 1+c2 |
| c |
∴椭圆方程为
| x2 |
| 2 |
(Ⅱ)由(Ⅰ)知F(1,0),
依题意FN⊥OM,MN⊥ON,
设N(x0,y0),则
| FN |
| OM |
| MN |
| ON |
则
| FN |
| OM |
| MN |
| ON |
由FN⊥OM,得2(x0-1)+ty0=0,
∴2x0+ty0=2,
由MN⊥ON,得x0(x0-2)+y0(y0-t)=0,
∴x02+y02=2x0+ty0=2,
∴|ON|=
| x02+y02 |
| 2 |
(Ⅲ)以OM为直径的圆的圆心为(1,
| t |
| 2 |
1+
|
圆心(1,
| t |
| 2 |
| |2t+2| |
| 5 |
又圆被直线3x-4y-5=0截得的弦长为2,
∴r2=d2+1,∴
| t2 |
| 4 |
| 4(t+1)2 |
| 25 |
∴圆的方程为(x-1)2+(y-2)2=5.
点评:本题考查椭圆方程的求法,考查线段长的求法,考查圆的方程的求法,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
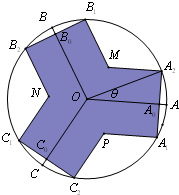 如图,半径为1的圆O,∠AOB=∠BOC=∠COA=
如图,半径为1的圆O,∠AOB=∠BOC=∠COA= 如图,将边长为1的正方形ABCD沿对角线AC折起,使得平面ADC⊥平面ABC,在折起后形成的三棱锥D-ABC中,给出下列三个命题:
如图,将边长为1的正方形ABCD沿对角线AC折起,使得平面ADC⊥平面ABC,在折起后形成的三棱锥D-ABC中,给出下列三个命题: