Question

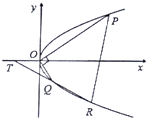如图，已知抛物线y²=x，过原点O作两条相互垂直的直线，分别交抛物线于点P，Q
（1）求证：直线PQ过定点，并求该定点的坐标．
（2）若过点Q的直线与抛物线的另一交点为R，与x轴的交点为T，且Q为线段RT的中点，求△PQT面积最小时，点Q的横坐标．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线中的最值与范围问题

分析：（1）设OP：y=kx，与抛物线y²=x交于P（

1

k2

，

1

k

），由OQ⊥OP，得Q（k²，-k），由此能求出PQ的方程，从而能证明PQ过定点M（1，0）．
（2）设T（k²+h，0），R（k²-h，-2k），R在抛物线上，从而培育出S_△PQT=

1

2

TM•|y_P-y_Q|=

1

2

（1+2k²）|

1

k

+k|，由此利用导数性质求出当k=土

-3+ 33 12

时，S_△PQT取最小值，从而能求出点Q的横坐标．

解答： （1）证明：设OP：y=kx，与抛物线y²=x交于P（

1

k2

，

1

k

），
∵OQ⊥OP，∴以-

1

k

代k，得Q（k²，-k），
∴PQ的斜率k_PQ=

1 k +k

1 k2 -k2

=

1

1 k -k

=

k

1-k2

，
∴PQ的方程：y+k=

k

1-k2

(x-k2)，
整理得kx+（k²-1）y-k=0，
∴PQ过定点M（1，0）．
（2）设T（k²+h，0），R（k²-h，-2k），
R在抛物线上，∴4k²k²-h，h=-3k²，∴T（-2k²，0），
∴S_△PQT=

1

2

TM•|y_P-y_Q|=

1

2

（1+2k²）|

1

k

+k|，
设f（k）=（1+2k²）•

1+k2

k

=2k³+3k+

1

k

，k＞0，
f'（k）=6k²+3-

1

k2

=

1

k2

（6k⁴+3k²-1）
=6（k²-

-3- 33

12

）（k²-

-3+ 33

12

）•

1

k2

，
当k=土

-3+ 33 12

时，S_△PQT取最小值，
∵Q（k²，-k），
∴△PQT面积最小时，点Q的横坐标xQ=

33 -3

12

．

点评：本题考查直线过定点坐标的证明，考查三角形面积最小时点的横坐标的求法，解题时要认真审题，注意导数性质的灵活运用．