题目内容
 某同学为了研究函数f(x)=
某同学为了研究函数f(x)=| 1+x2 |
| 1+(1-x)2 |
(1)fmin(x)=
(2)函数f(x)=
| ||
| 2 |
考点:函数零点的判定定理
专题:数形结合
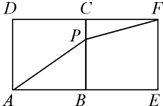
分析:(1)通过数形结合知道RT△AEF的斜边AF的长就是函数的最小值,求出即可;(2)通过分析图象可得满足条件的P点有两个,故有两个零点.
解答:
解;(1)当A,P,F在同一直线上时,f(x)最小,
此时,AF=
=
=
;
故答案为:
.
(2)如图示:
 ,
,
当平行四边形AP1FP2的周长为
时,
即AP1+P1F=AP2+P2F=
满足题意,
∴函数f(x)=
的零点个数是2个,
故答案为:2个.
此时,AF=
| AE2+EF2 |
| 22+12 |
| 5 |
故答案为:
| 5 |
(2)如图示:
 ,
,当平行四边形AP1FP2的周长为
| 22 |
即AP1+P1F=AP2+P2F=
| ||
| 2 |
∴函数f(x)=
| ||
| 2 |
故答案为:2个.
点评:本题考察了函数的零点问题,渗透了数形结合思想,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,将边长为1的正方形ABCD沿对角线AC折起,使得平面ADC⊥平面ABC,在折起后形成的三棱锥D-ABC中,给出下列三个命题:
如图,将边长为1的正方形ABCD沿对角线AC折起,使得平面ADC⊥平面ABC,在折起后形成的三棱锥D-ABC中,给出下列三个命题:
