题目内容
9.已知实数a,b满足不等式log2a<log3b,则下列结论:①0<b<a<1②0<a<b<1③1<a<b④1<b<a其中可能成立的有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 实数a,b满足不等式log2a<log3b,画出函数y=log2x,y=log3x的图象,即可得出.
解答 解:∵实数a,b满足不等式log2a<log3b,画出函数y=log2x,y=log3x的图象:
则下列结论:①0<b<a<1;②0<a<b<1;③1<a<b;
④1<b<a.
其中可能成立的有①③.
故选:B.
点评 本题考查了对数函数的单调性、数形结合方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.已知向量$\overrightarrow a=(2k-3,-6)$,$\overrightarrow b=(2,1)$,且$\overrightarrow a⊥\overrightarrow b$,则实数k的值为( )
| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
20.已知△ABC中,D为边BC上靠近B点的三等分点,连接AD,E为线段AD的中点,若$\overrightarrow{CE}=m\overrightarrow{AB}+n\overrightarrow{AC}$,则m+n=( )
| A. | $-\frac{1}{3}$ | B. | $-\frac{1}{2}$ | C. | $-\frac{1}{4}$ | D. | $\frac{1}{2}$ |
17.要使函数$y={(\frac{1}{2})^x}$+m的图象不经过第一象限,则m的取值范围是( )
| A. | m≥-1 | B. | m≤-1 | C. | m≤-2 | D. | m≥-2 |
1.已知R是实数集,A={y|y=2x-1,x∈R},B={x|y=log2(1-x2)},则A∩B=( )
| A. | (-1,+∞) | B. | (-1,1) | C. | [-1,1) | D. | (1,+∞) |
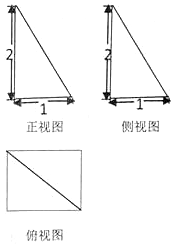 已知四棱锥P-ABCD,PA⊥底面ABCD,其三视图如下,若M是PD的中点.
已知四棱锥P-ABCD,PA⊥底面ABCD,其三视图如下,若M是PD的中点.