题目内容
14．一投资公司有300万元资金，准备投资A、B两个项目，按照合同要求，对项目A的投资不少于对项目B的三分之二，而且每个项目的投资不少于25万元，若对项目A投资1万元可获利润0.4万元，对项目B投资1万元可获利润0.6万元，求该公司在这两个项目上共可获得的最大利润是多少？分析 这是一个简单的投资分析，由题意，设对A投资x万元，对B投资y万元．利润为z万元，得到x，y的约束条件，以及目标函数，画出可行域，利用目标函数的几何意义求z最大值．
解答 解：设对A投资x万元，对B投资y万元．利润为z万元，则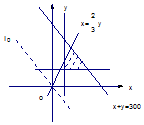
$\left\{\begin{array}{l}{x≥\frac{2}{3}y}\\{x≥25}\\{y≥25}\\{x+y≤300}\end{array}\right.$，
设z=0.4x+0.6y，
作出可行域，如图所示，平移直线l0：y=-$\frac{2}{3}x$，当过点A（120，180）时，取得最大值．且最大值zmax=0.4×120+0.6×180=156万元．
答：该公司在这两个项目上共可获得的最大利润是156万元．
点评 用图解法解决线性规划问题时，分析题目的已知条件，找出约束条件和目标函数是关键，可先将题目中的量分类、列出表格，理清头绪，然后列出不等式组（方程组）寻求约束条件，并就题目所述找出目标函数．然后将可行域各角点的值一一代入，最后比较，即可得到目标函数的最优解．
练习册系列答案
相关题目
4．下列命题（a，b表示直线，α表示平面）中正确的是（ ）
| A． | $\left.{\frac{a||b}{b⊥α}}\right\}⇒a⊥α$ | B． | $\left.{\frac{a||b}{b?α}}\right\}⇒a||α$ | C． | $\left.\begin{array}{l}a⊥b\\ b∥α\end{array}\right\}⇒a⊥α$ | D． | $\left.\begin{array}{l}a⊥α\\ a⊥b\end{array}\right\}⇒b?α$ |
5．已知A，B是球O的球面上两点，∠AOB=90°，C为该球面上的动点，若三棱锥O-ABC体积的最大值为36，则球O的体积为（ ）
| A． | 72π | B． | 144π | C． | 288π | D． | 576π |
6．已知全集U={1，2，3，4，5，6，7，8}，集合A={2，3，5，6}，集合B={1，3，4，7}，则集合A∩（∁UB）=（ ）
| A． | {2，5} | B． | {3，6} | C． | {2，5，6} | D． | {2，3，5，6，8} |
3．已知数列{an}，an=|n-1|+|n-2|+…|n-20|，n∈N+，且1≤n≤20，则a5=（ ）
| A． | 190 | B． | 160 | C． | 130 | D． | 10 |