题目内容
4.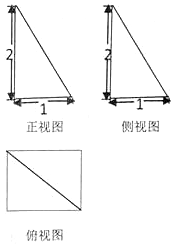 已知四棱锥P-ABCD,PA⊥底面ABCD,其三视图如下,若M是PD的中点.
已知四棱锥P-ABCD,PA⊥底面ABCD,其三视图如下,若M是PD的中点.(1)求证:PB∥平面MAC;
(2)求证:CD⊥平面PAD;
(3)求直线CM与平面PAD所成角的正弦值.
分析 (1)由三视图还原原图形,可得四棱锥P-ABCD的底面为正方形,连接AC,BD相交于O,则BO=DO,又M为PD的中点,由三角形中位线定理可得OM∥PB,再由线面平行的判定可得PB∥平面MAC;
(2)由已知PA⊥平面ABCD,得PA⊥CD,结合ABCD为正方形,得CD⊥AD,由线面垂直的判定可得CD⊥平面PAD;
(3)由(2)知,∠CMD为直线CM与平面PAD所成角.求解直角三角形得答案.
解答 (1)证明:由三视图还原原几何体如图,PA⊥平面ABCD,底面ABCD为正方形.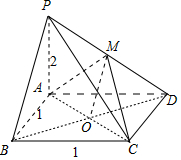
连接AC,BD相交于O,则BO=DO,又M为PD的中点,
连接OM,则OM∥PB,
∵OM?平面AMC,PB?平面AMC,
∴PB∥平面MAC;
(2)证明:∵PA⊥平面ABCD,∴PA⊥CD,
又ABCD为正方形,∴CD⊥AD,
又PA⊥AD=A,
∴CD⊥平面PAD;
(3)由(2)知,∠CMD为直线CM与平面PAD所成角.
∵PA=2,AD=1,∴PD=$\sqrt{5}$,则MD=$\frac{\sqrt{5}}{2}$,
∴MC=$\sqrt{(\frac{\sqrt{5}}{2})^{2}+{1}^{2}}=\frac{3}{2}$,则sin∠CMD=$\frac{CD}{CM}=\frac{1}{\frac{3}{2}}=\frac{2}{3}$.
∴直线CM与平面PAD所成角的正弦值$\frac{2}{3}$.
点评 本题考查直线与平面平行、直线与平面垂直的判定,考查线面角的求法,考查空间想象能力和思维能力,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.若点P在y=x2上,点Q在x2+(y-3)2=1上,则|PQ|的最小值为( )
| A. | $\sqrt{3}$-1 | B. | $\frac{\sqrt{11}}{2}$-1 | C. | 2 | D. | $\frac{\sqrt{10}}{2}$-1 |
16.已知f(x)=$\left\{\begin{array}{l}{{a}^{x}-a,x>1}\\{{x}^{2}+\frac{1}{2}ax-2,x≤1}\end{array}\right.$是(-$\frac{3}{8}$,+∞)上的增函数,那么a的取值范围是( )
| A. | ($\frac{3}{2}$,2) | B. | (1,2] | C. | [$\frac{3}{2}$,2] | D. | (1,2) |
13.已知集合M={第一象限角},N={锐角},P={小于90°角},则下列关系式中正确的是( )
| A. | M=N=P | B. | M?P=N | C. | M∩P=N | D. | N∩P=N |
4.已知函数f(x)=x4-4x3+10x2-27,则方程f(x)=0在[2,10]上的根( )
| A. | 有3个 | B. | 有2个 | C. | 有且只有1个 | D. | 不存在 |