Question

20．已知△ABC中，D为边BC上靠近B点的三等分点，连接AD，E为线段AD的中点，若$\overrightarrow{CE}=m\overrightarrow{AB}+n\overrightarrow{AC}$，则m+n=（　　）

• A． $-\frac{1}{3}$
• B． $-\frac{1}{2}$
• C． $-\frac{1}{4}$
• D． $\frac{1}{2}$

Answer 1

分析 根据题意画出图形，结合图形，利用平面向量的线性运算性质，用$\overrightarrow{AB}$、$\overrightarrow{AC}$表示出$\overrightarrow{CD}$、$\overrightarrow{CE}$，求出m、n的值即可．

解答 解：如图所示，△ABC中，D为边BC上靠近B点的三等分点，E为线段AD的中点，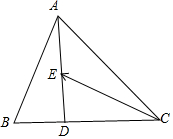

∴$\overrightarrow{CB}$=$\overrightarrow{AB}$-$\overrightarrow{AC}$，
∴$\overrightarrow{CD}$=$\frac{2}{3}$$\overrightarrow{CB}$=$\frac{2}{3}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AC}$；
∴$\overrightarrow{CE}$=$\frac{1}{2}$（$\overrightarrow{CD}$+$\overrightarrow{CA}$）
=$\frac{1}{2}$$\overrightarrow{CD}$-$\frac{1}{2}$$\overrightarrow{AC}$
=$\frac{1}{3}$$\overrightarrow{AB}$-$\frac{1}{3}$$\overrightarrow{AC}$-$\frac{1}{2}$$\overrightarrow{AC}$
=$\frac{1}{3}$$\overrightarrow{AB}$-$\frac{5}{6}$$\overrightarrow{AC}$；
又$\overrightarrow{CE}=m\overrightarrow{AB}+n\overrightarrow{AC}$，
∴m=$\frac{1}{3}$，n=-$\frac{5}{6}$；
∴m+n=-$\frac{1}{2}$．
故选：B．

点评 本题考查了平面向量的线性运算性质的应用问题，也考查了推理与运算能力，是基础题目．