题目内容
设集合S={x|x＜1}，T={x|x≤2}，则S∩T= ；S∪T= ；T∩∁RS= ．（R表示实数集）
考点：交、并、补集的混合运算,交集及其运算
专题：集合
分析：根据交集并集补集的概念，即可求出
解答：
解：∵S={x|x＜1}，T={x|x≤2}，
∴∁RS═{x|x≥1}，
∴S∩T={x|x＜1}=（-∞，1），
S∪T={x|x≤2}=（-∞，2]，
T∩∁RS={x|1≤x≤2}=[1，2]，
故答案为：（-∞，1），（-∞，2]，[1，2]
∴∁RS═{x|x≥1}，
∴S∩T={x|x＜1}=（-∞，1），
S∪T={x|x≤2}=（-∞，2]，
T∩∁RS={x|1≤x≤2}=[1，2]，
故答案为：（-∞，1），（-∞，2]，[1，2]
点评：此题考查了交、并、补集的混合运算，熟练掌握各自的定义是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
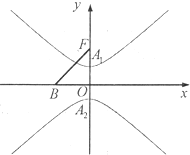已知点A1，A2是双曲线| y2 |
| a2 |
| x2 |
| b2 |
A、（1，
| ||||||
B、（1，
| ||||||
C、（
| ||||||
D、（
|
已知函数g（x）=a-x2（
≤x≤e，e为自然对数的底数）与h（x）=2lnx的图象上存在关于x轴对称的点，则实数a的取值范围是（ ）
| 1 |
| e |
A、[1，
| ||
| B、[1，e2-2] | ||
C、[
| ||
| D、[e2-2，+∞） |