题目内容
已知函数g(x)=a-x2(
≤x≤e,e为自然对数的底数)与h(x)=2lnx的图象上存在关于x轴对称的点,则实数a的取值范围是( )
| 1 |
| e |
A、[1,
| ||
| B、[1,e2-2] | ||
C、[
| ||
| D、[e2-2,+∞) |
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:由已知,得到方程a-x2=-2lnx?-a=2lnx-x2在[
,e]上有解,构造函数f(x)=2lnx-x2,求出它的值域,得到-a的范围即可.
| 1 |
| e |
解答:
解:由已知,得到方程a-x2=-2lnx?-a=2lnx-x2在[
,e]上有解.
设f(x)=2lnx-x2,求导得:f′(x)=
-2x=
,
∵
≤x≤e,∴f′(x)=0在x=1有唯一的极值点,
∵f(
)=-2-
,f(e)=2-e2,f(x)极大值=f(1)=-1,且知f(e)<f(
),
故方程-a=2lnx-x2在[
,e]上有解等价于2-e2≤-a≤-1.
从而a的取值范围为[1,e2-2].
故选B.
| 1 |
| e |
设f(x)=2lnx-x2,求导得:f′(x)=
| 2 |
| x |
| 2(1-x)(1+x) |
| x |
∵
| 1 |
| e |
∵f(
| 1 |
| e |
| 1 |
| e2 |
| 1 |
| e |
故方程-a=2lnx-x2在[
| 1 |
| e |
从而a的取值范围为[1,e2-2].
故选B.
点评:本题考查了构造函数法求方程的解及参数范围;关键是将已知转化为方程a-x2=-2lnx?-a=2lnx-x2在[
,e]上有解.
| 1 |
| e |

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
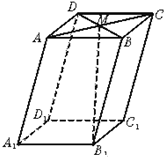 如图,在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点.若
如图,在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点.若| A1B1 |
| a |
| A1D1 |
| b |
| A1A |
| c |
| B1M |
A、-
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、-
|
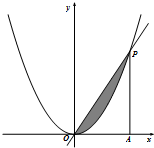 如图,直线y=kx(k>0)与函数y=x2的图象交于点O,P,过P作PA⊥x轴于A.在△OAP中任取一点,则该点落在阴影部分的概率为
如图,直线y=kx(k>0)与函数y=x2的图象交于点O,P,过P作PA⊥x轴于A.在△OAP中任取一点,则该点落在阴影部分的概率为 如图所示,向量
如图所示,向量