题目内容
某联欢晚会矩形抽奖活动,举办方设置了甲乙两种抽奖方案,方案甲的中奖率为
,中奖可以获得2分,方案乙的中奖率为
,中奖可以得3分,未中奖则不得分,每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
(1)若小明选择方案甲,小红选择方案乙,记他们的累计得分为X,求X<4的概率;
(2)若小明小红两人选择同一方案抽奖,问:他们选择何种方案抽奖,累计得分的数学期望最大?
| 2 |
| 3 |
| 2 |
| 5 |
(1)若小明选择方案甲,小红选择方案乙,记他们的累计得分为X,求X<4的概率;
(2)若小明小红两人选择同一方案抽奖,问:他们选择何种方案抽奖,累计得分的数学期望最大?
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:概率与统计
分析:(1)记“这两人的累计得分X<4”的事件为A,则事件A的对立事件为“X=5”,由此能求出这两人的累计得分X<4的概率.
(2)设小明、小红都选择方案甲抽奖中奖的次数为ξ,都选择方案乙抽奖中奖的次数为η,则这两人选择方案甲抽奖累计得分的数学期望为E(2ξ),选择方案乙抽奖累计得分的数学期望为E(3η),由此能求出他们选择甲种方案抽奖,累计得分的数学期望最大.
(2)设小明、小红都选择方案甲抽奖中奖的次数为ξ,都选择方案乙抽奖中奖的次数为η,则这两人选择方案甲抽奖累计得分的数学期望为E(2ξ),选择方案乙抽奖累计得分的数学期望为E(3η),由此能求出他们选择甲种方案抽奖,累计得分的数学期望最大.
解答:
解:(1)记“这两人的累计得分X<4”的事件为A,则事件A的对立事件为“X=5”,
∵P(X=5)=
×
=
,
∴P(A)=1-P(X=5)=1-
=
,
∴这两人的累计得分X<4的概率为
.
(2)设小明、小红都选择方案甲抽奖中奖的次数为ξ,都选择方案乙抽奖中奖的次数为η,
则这两人选择方案甲抽奖累计得分的数学期望为E(2ξ),
选择方案乙抽奖累计得分的数学期望为E(3η),
由已知得ξ~B(2,
),η~B(2,
),
∴E(ξ)=2×
=
,E(η)=2×
=
,
∴E(2ξ)=
>E(3η)=
,
∴他们选择甲种方案抽奖,累计得分的数学期望最大.
∵P(X=5)=
| 2 |
| 3 |
| 2 |
| 5 |
| 4 |
| 15 |
∴P(A)=1-P(X=5)=1-
| 4 |
| 15 |
| 11 |
| 15 |
∴这两人的累计得分X<4的概率为
| 11 |
| 15 |
(2)设小明、小红都选择方案甲抽奖中奖的次数为ξ,都选择方案乙抽奖中奖的次数为η,
则这两人选择方案甲抽奖累计得分的数学期望为E(2ξ),
选择方案乙抽奖累计得分的数学期望为E(3η),
由已知得ξ~B(2,
| 2 |
| 3 |
| 2 |
| 5 |
∴E(ξ)=2×
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 5 |
| 4 |
| 5 |
∴E(2ξ)=
| 8 |
| 3 |
| 12 |
| 5 |
∴他们选择甲种方案抽奖,累计得分的数学期望最大.
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型之一.

练习册系列答案
相关题目
函数f(x)=asinx+blog2(x+
)+4(a、b为常数),若f(x)在(0,+∞)上有最小值-4,则f(x)在(-∞,0)上有( )
| x2+1 |
| A、最大值-2 |
| B、最大值 4 |
| C、最大值10 |
| D、最大值12 |
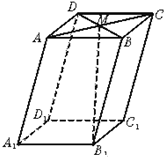 如图,在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点.若
如图,在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点.若| A1B1 |
| a |
| A1D1 |
| b |
| A1A |
| c |
| B1M |
A、-
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、-
|
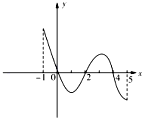 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.
已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.| x | -1 | 0 | 2 | 4 | 5 |
| y | 1 | 2 | 0 | 2 | 1 |
| A、[1,2) |
| B、[1,2] |
| C、(2,3) |
| D、[1,3) |