题目内容
下列结论正确的是( )
①“a=1”是“直线x-ay=0与直线x+ay=0互相垂直”的充要条件
②函数f(x)=sin(2x-
)最小正周期为π,且图象关于直线x=
对称
③线性回归直线至少经过样本点中的一个
④?x∈R,2x-1≥0的否定是?x∈R,2x-1<0.
①“a=1”是“直线x-ay=0与直线x+ay=0互相垂直”的充要条件
②函数f(x)=sin(2x-
| π |
| 6 |
| π |
| 3 |
③线性回归直线至少经过样本点中的一个
④?x∈R,2x-1≥0的否定是?x∈R,2x-1<0.
| A、② | B、②④ | C、①②③ | D、①②④ |
考点:命题的真假判断与应用
专题:计算题,函数的性质及应用,直线与圆,简易逻辑
分析:由两直线垂直的条件,计算即可得到a,即可判断①;
由正弦函数的周期公式和对称轴方程,即可判断②;
由线性回归直线必然经过点(
,
),但不一定经过(xn,yn),即可判断③;
由命题的否定形式,即可判断④.
由正弦函数的周期公式和对称轴方程,即可判断②;
由线性回归直线必然经过点(
. |
| x |
| y |
由命题的否定形式,即可判断④.
解答:
解:对于①,直线x-ay=0与直线x+ay=0互相垂直,则1-a2=0,即a=±1,则①错误;
对于②,函数f(x)=sin(2x-
)最小正周期为
=π,由sin(2×
-
)=sin
=1,
则图象关于直线x=
对称,则②正确;
对于③,线性回归直线必然经过点(
,
),但不一定经过(xn,yn),则③错误;
对于④,?x∈R,2x-1≥0的否定是?x∈R,2x-1<0,则④正确.
故选B.
对于②,函数f(x)=sin(2x-
| π |
| 6 |
| 2π |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
则图象关于直线x=
| π |
| 3 |
对于③,线性回归直线必然经过点(
. |
| x |
| y |
对于④,?x∈R,2x-1≥0的否定是?x∈R,2x-1<0,则④正确.
故选B.
点评:本题考查两直线垂直的条件、正弦函数的周期和对称性,考查命题的否定和线性回归直线的特点,考查判断能力,属于基础题和易错题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
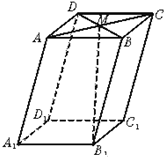 如图,在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点.若
如图,在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点.若| A1B1 |
| a |
| A1D1 |
| b |
| A1A |
| c |
| B1M |
A、-
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、-
|
设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )
| A、若m∥n,n?α则 m∥α |
| B、若m?α,α⊥β,则m⊥β |
| C、若m∥n,m⊥α,则n⊥α |
| D、若m⊥n,m?α,n?β,则α⊥β |
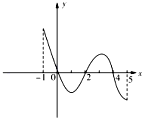 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.
已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.| x | -1 | 0 | 2 | 4 | 5 |
| y | 1 | 2 | 0 | 2 | 1 |
| A、[1,2) |
| B、[1,2] |
| C、(2,3) |
| D、[1,3) |
设tanα、tanβ是方程x2+x-2=0的两实数根,则tan(α+β)的值为( )
| A、-1 | ||
B、-
| ||
C、
| ||
| D、1 |
 如图,某商业中心O有通往正东方向和北偏东30°方向的两条街道,某公园P位于商业中心北偏东θ角(0<θ<
如图,某商业中心O有通往正东方向和北偏东30°方向的两条街道,某公园P位于商业中心北偏东θ角(0<θ<