题目内容
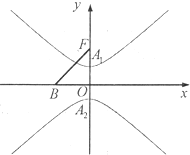 已知点A1,A2是双曲线
已知点A1,A2是双曲线| y2 |
| a2 |
| x2 |
| b2 |
A、(1,
| ||||||
B、(1,
| ||||||
C、(
| ||||||
D、(
|
考点:双曲线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:求出直线BF的方程为bx+cy-bc=0,利用直线与圆的位置关系,结合a<b,即可求出双曲线离心率e的取值范围.
解答:
解:由题意,F(0,c),B(-b,0),则直线BF的方程为cx-by+bc=0,
∵在线段BF上(不含端点)存在不同的两点P,Q,使得△PA1A2,△QA1A2都是以A1A2为斜边的直角三角形,
∴
<a,
∴e4-3e2+1<0,
∵e>1,
∴e<
又∵a<b,
∴a2<c2-a2,
∴e>
,
∴
<e<
.
故选:D.
∵在线段BF上(不含端点)存在不同的两点P,Q,使得△PA1A2,△QA1A2都是以A1A2为斜边的直角三角形,
∴
| bc | ||
|
∴e4-3e2+1<0,
∵e>1,
∴e<
| ||
| 2 |
又∵a<b,
∴a2<c2-a2,
∴e>
| 2 |
∴
| 2 |
| ||
| 2 |
故选:D.
点评:本题考查双曲线的简单性质,考查离心率,考查直线与圆的位置关系,属于中档题.

练习册系列答案
相关题目
若某几何体的三视图如图所示,则这个几何体的体积为( )
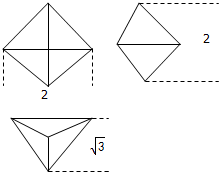

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知直线l⊥平面α,直线m?平面β,有下列四个命题:
①若α∥β,则l⊥m;
②若α⊥β,则l∥m;
③若l∥m,则α⊥β;
④若l⊥m,则α∥β.
以上命题中,正确命题的序号是( )
①若α∥β,则l⊥m;
②若α⊥β,则l∥m;
③若l∥m,则α⊥β;
④若l⊥m,则α∥β.
以上命题中,正确命题的序号是( )
| A、①② | B、①③ | C、②④ | D、③④ |
函数f(x)=asinx+blog2(x+
)+4(a、b为常数),若f(x)在(0,+∞)上有最小值-4,则f(x)在(-∞,0)上有( )
| x2+1 |
| A、最大值-2 |
| B、最大值 4 |
| C、最大值10 |
| D、最大值12 |
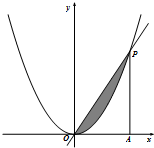 如图,直线y=kx(k>0)与函数y=x2的图象交于点O,P,过P作PA⊥x轴于A.在△OAP中任取一点,则该点落在阴影部分的概率为
如图,直线y=kx(k>0)与函数y=x2的图象交于点O,P,过P作PA⊥x轴于A.在△OAP中任取一点,则该点落在阴影部分的概率为