题目内容
下列关于两条不同的直线l,m两个不重合的平面α,β的说法,正确的是( )
| A、若l?α且α⊥β,则l⊥β |
| B、若l⊥β且m⊥β,则l∥m |
| C、若l⊥β且α⊥β,则l∥α |
| D、若α∩β=m且l⊥m,则l⊥α |
考点:命题的真假判断与应用,空间中直线与直线之间的位置关系,空间中直线与平面之间的位置关系,直线与平面垂直的判定
专题:
分析:在分析题目时可结合着图象判断,解题时应就线面关系平行,相交及在其内考查的更全面.
解答:
解:由线面垂直的判定定理,即“垂直于同一个平面的两条直线平行可知”,选择B.
在选项A中,由条件可得,l∥β或l?β或l与β相交;
在选项C中,由条件可得,l∥α或l?α;
在选项D中,由条件可得,l∥α或l?α或l与α相交.
故答案选B.
在选项A中,由条件可得,l∥β或l?β或l与β相交;
在选项C中,由条件可得,l∥α或l?α;
在选项D中,由条件可得,l∥α或l?α或l与α相交.
故答案选B.
点评:在本题的处理中,可以针对于单项选择题的特性,用确定的方法,根据定理直接锁定B选项.

练习册系列答案
相关题目
复数z=
在复平面上对应的点的坐标为( )
| 1-i |
| 2+i |
| A、(1,-3) | ||||
B、(
| ||||
| C、(3,-3) | ||||
D、(
|
已知f(x)=
定义域为M,g(x)=ex值域为N,则M∩N=( )
| 1-x |
| A、[0,1] |
| B、(0,1] |
| C、(0,+∞) |
| D、[1,+∞) |
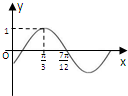 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<| π |
| 2 |
| π |
| 6 |
A、{x|x=kπ-
| ||
B、{x|x=kπ-
| ||
C、{x|x=2kπ-
| ||
D、{x|x=2kπ-
|
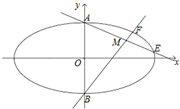 已知椭圆Γ:
已知椭圆Γ: