题目内容
已知椭圆E:
+
=1的上顶点为A,直线y=-4交椭圆E于点B,C(点B在点C的左侧),点P在椭圆E上.
(Ⅰ)求以原点O为顶点,椭圆的右焦点为焦点的抛物线的方程;
(Ⅱ)求以原点O为圆心,与直线AB相切的圆的方程;
(Ⅲ)若四边形ABCP为梯形,求点P的坐标.
| x2 |
| 100 |
| y2 |
| 25 |
(Ⅰ)求以原点O为顶点,椭圆的右焦点为焦点的抛物线的方程;
(Ⅱ)求以原点O为圆心,与直线AB相切的圆的方程;
(Ⅲ)若四边形ABCP为梯形,求点P的坐标.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)由题意设出抛物线方程,由椭圆方程求得椭圆的右焦点坐标,代入抛物线方程求得P,则抛物线方程可求;
(Ⅱ)由椭圆方程求得上顶点A的坐标,把y=-4代入椭圆方程求出B,C的坐标,求出直线AB的方程,由原点O到直线AB的距离得到所求圆的半径,则圆的方程可求;
(Ⅲ)由题意可知,要使四边形ABCP为梯形,当且仅当CP∥AB,由此求出CP的方程,和椭圆联立求得P点的坐标.
(Ⅱ)由椭圆方程求得上顶点A的坐标,把y=-4代入椭圆方程求出B,C的坐标,求出直线AB的方程,由原点O到直线AB的距离得到所求圆的半径,则圆的方程可求;
(Ⅲ)由题意可知,要使四边形ABCP为梯形,当且仅当CP∥AB,由此求出CP的方程,和椭圆联立求得P点的坐标.
解答:
解:(Ⅰ)设此抛物线的方程为y2=2px,
由椭圆E:
+
=1,
得椭圆的右焦点为(5
,0),
∴
=5
,即p=10
.
∴此抛物线的方程为y2=20
x;
(Ⅱ)由条件知:A(0,5),B(-6,-4),
∴kAB=
.
∴直线AB的方程:y=
x+5,即3x-2y+10=0.
∴O到直线AB的距离为
=
,即圆半径r=
.
∴以原点O为圆心,与直线AB相切的圆的方程x2+y2=
;
(Ⅲ)要使四边形ABCP为梯形,当且仅当CP∥AB,
∴kCP=kAB=
.
∴直线CP的方程为y+4=
(x-6),即y=
x-13.
把y=
x-13代入
+
=1,得:5x2-78x+288=0.
解得:x=6或x=
.
∴P(
,
).
由椭圆E:
| x2 |
| 100 |
| y2 |
| 25 |
得椭圆的右焦点为(5
| 3 |
∴
| p |
| 2 |
| 3 |
| 3 |
∴此抛物线的方程为y2=20
| 3 |
(Ⅱ)由条件知:A(0,5),B(-6,-4),
∴kAB=
| 3 |
| 2 |
∴直线AB的方程:y=
| 3 |
| 2 |
∴O到直线AB的距离为
| |10| | ||
|
10
| ||
| 13 |
10
| ||
| 13 |
∴以原点O为圆心,与直线AB相切的圆的方程x2+y2=
| 100 |
| 13 |
(Ⅲ)要使四边形ABCP为梯形,当且仅当CP∥AB,
∴kCP=kAB=
| 3 |
| 2 |
∴直线CP的方程为y+4=
| 3 |
| 2 |
| 3 |
| 2 |
把y=
| 3 |
| 2 |
| x2 |
| 100 |
| y2 |
| 25 |
解得:x=6或x=
| 48 |
| 5 |
∴P(
| 48 |
| 5 |
| 7 |
| 5 |
点评:本题考查抛物线方程的求法,考查直线与抛物线的位置关系的应用,训练了点到直线的距离公式,考查了两直线平行的条件,是中档题.

练习册系列答案
相关题目
设m,n∈R,若直线(m-1)x+(n-1)y+2=0与圆(x-1)2+(y-1)2=1相切,则m+n的取值范围是( )
A、[-2-2
| ||||
B、[2-2
| ||||
C、(-∞,-2-2
| ||||
D、(-∞,2-2
|
复数z=
在复平面上对应的点的坐标为( )
| 1-i |
| 2+i |
| A、(1,-3) | ||||
B、(
| ||||
| C、(3,-3) | ||||
D、(
|
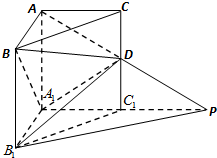 如图,在直三棱柱ABC-A1B1C1中,BC=
如图,在直三棱柱ABC-A1B1C1中,BC= 如图所示,ABCDEF是边长为1的正六边形,现从六个顶点任取三个顶点构成三角形,该三角形的面积S是一随机变量.
如图所示,ABCDEF是边长为1的正六边形,现从六个顶点任取三个顶点构成三角形,该三角形的面积S是一随机变量.