题目内容
过圆x2+y2=1上一点作圆的切线与x轴、y轴的正半轴交于A、B两点,则|AB|的最小值为 .
考点:直线与圆的位置关系
专题:直线与圆
分析:用截距式设出切线方程,由圆心到直线的距离等于半径以及基本不等式可得:
,令t=
,可得t的最小值为 2,进而得到答案.
| a2+b2 |
| a2+b2 |
解答:
解:设切线方程为
+
=1(a>0,b>0),即 bx+ay-ab=0,
∵圆心(0,0)到直线的距离等于半径得
=1,
∴ab=
≤
,
令t=
,则有t2-2t≥0,t≥2,
则t的最小值为2,即|AB|的最小值为2.
故答案为:2
| x |
| a |
| y |
| b |
∵圆心(0,0)到直线的距离等于半径得
| |0+0-ab| | ||
|
∴ab=
| a2+b2 |
| a2+b2 |
| 2 |
令t=
| a2+b2 |
则t的最小值为2,即|AB|的最小值为2.
故答案为:2
点评:此题考查了直线与圆的位置关系,涉及的知识有:点到直线的距离公式,基本不等式的运用,直线的截距式方程,利用了换元的思想,熟练掌握公式及性质是解本题的关键.

练习册系列答案
相关题目
实验测得四组(x,y)的值是(1,2),(2,4),(3,4),(4,5),(5,5),若线性回归方程是
=0.7x+
.则
的值是( )
 |
| y |
 |
| a |
 |
| a |
| A、1.9 | B、1.4 |
| C、2.6 | D、2.2 |
已知f(x)=
定义域为M,g(x)=ex值域为N,则M∩N=( )
| 1-x |
| A、[0,1] |
| B、(0,1] |
| C、(0,+∞) |
| D、[1,+∞) |
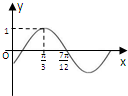 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<| π |
| 2 |
| π |
| 6 |
A、{x|x=kπ-
| ||
B、{x|x=kπ-
| ||
C、{x|x=2kπ-
| ||
D、{x|x=2kπ-
|
 如图,△ABC的三条角平分线交于点O,过点O作OE⊥BC于点E,求证:∠BOD=∠COE.
如图,△ABC的三条角平分线交于点O,过点O作OE⊥BC于点E,求证:∠BOD=∠COE.