题目内容
已知函数f（x）=x2+4x+5，若二次函数y=g（x）满足：①y=f（x）与y=g（x）的图象在点P（1，10）处有公共切线；②y=f（x）+g（x）是R上的单调函数．则g（x）= ．
考点：二次函数的性质,函数解析式的求解及常用方法
专题：函数的性质及应用
分析：先根据f（x）求出在点P（1，10）的切线，再由y=f（x）+g（x）是R上的单调函数设g（x）=-x2+bx+c，再根据两个函数在该点求导有f′（1）=g′（1）．再由点在y=g（x）上求得c．
解答：
解：由f（x）=x2+4x+5，得到f′（x）=2x+4，
∴f′（1）=6，
设g（x）=-x2+bx+c，则有g′（x）=2ax+b，则有g′（1）=-2+b=6，即b=8．
又点P（1，10）也在y=g（x）上，有-12+8×1+c=10，∴c=3．
∴g（x）=-x2+8x+3
故答案为：-x2+8x+3
∴f′（1）=6，
设g（x）=-x2+bx+c，则有g′（x）=2ax+b，则有g′（1）=-2+b=6，即b=8．
又点P（1，10）也在y=g（x）上，有-12+8×1+c=10，∴c=3．
∴g（x）=-x2+8x+3
故答案为：-x2+8x+3
点评：本题考查二次函数解析式，还考查了导数求切线的知识点．
练习册系列答案
相关题目
函数f（x）=lnx2（ ）
| A、是偶函数且在（-∞，0）上单调递增 |
| B、是偶函数且在（0，+∞）上单调递增 |
| C、是奇函数且在（0，+∞）上单调递减 |
| D、是奇函数且在（-∞，0）上单调递减 |
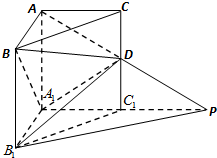如图，在直三棱柱ABC-A1B1C1中，BC=
如图所示，ABCDEF是边长为1的正六边形，现从六个顶点任取三个顶点构成三角形，该三角形的面积S是一随机变量．