题目内容

若角β的终边经过点P（1，-2），则sinβ的值是（　　）
A、-
2
5
5
B、
5
5
C、-
5
5
D、
2
5
5
考点：任意角的三角函数的定义
专题：计算题,三角函数的求值
分析：由角β的终边经过点P（1，-2），利用任意角的三角函数定义求出sinβ即可．
解答： 解：∵角β的终边经过点P（1，-2），
∴x=1，y=-2，|OP|=
5
，
因此，sinβ=
-2
5
=-
2
5
5
．
故选：A．
点评：此题考查了任意角的三角函数定义，熟练掌握三角函数的定义是解本题的关键．
练习册系列答案
相关题目
已知sinα=
4
3
7
，sin（α-β）=
3
3
14
，且0＜β＜α＜
π
2
．
（Ⅰ）求tan2α的值；
（Ⅱ）求角β的值．
已知函数f（x）=
2x-1
2x+1
（x∈R）．
（1）求函数f（x）的值域；    
（2）①判断并证明函数f（x）的奇偶性；②判断并证明函数f（x）的单调性；   
（3）解不等式f（1-m）+f（1-m2）＜0．
函数f（x）=ax3-6ax2+b（a＞0）在区间[-1，2]上的最大值为3，最小值为-29，则（　　）
A、a=2，b=-29
B、a=3，b=2
C、a=2，b=3
D、以上都不对
设等差数列{an}的前n项和为Sn，若a1=-3，ak+1=
3
2
，Sk=-12，则正整数k=（　　）
A、10B、11C、12D、13
设函数f（x）=logax（a＞0，且a≠1）在（0，+∞）上单调递增，则f（a+1）与f（2）的大小关系是（　　）
A、f（a+1）=f（2）
B、f（a+1）＞f（2）
C、f（a+1）＜f（2）
D、不确定
设集合A={（x，y）|y=x2+4x+6}，B={（x，y）|y=2x+a}，问：
（1）a为何值时，集合A∩B有两个元素；
（2）a为何值时，集合A∩B至多有一个元素．
已知奇函数f（x）的定义域为（-∞，0）∪（0，+∞），且f（x）在（0，+∞）上是增函数，f（1）=0．
（1）求证：函数f（x）在（-∞，0）上是增函数；
（2）解关于x的不等式f（x）＜0．
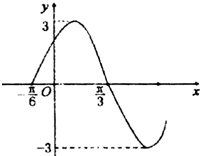
如图所示是y=Asin（ωx+φ）的图象（其中A＞0，ω＞0，|φ|≤
π
2
）一部分，则其解析表达式为（　　）
A、y=3cos（2x+
π
3
）
B、y=3cos（2x-
π
3
）
C、y=3sin（2x+
π
3
）
D、y=3sin（2x-
π
3
）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网